Алгебраические структуры на целых числах

Покажем некоторые интересные свойства приведенной системы вычетов. Но сначала напомним определения группы, кольца и поля.

Примечание: операция называется заданной на множестве, если результат применения этой операции к любым элементам множества также принадлежит этому множеству.

Группой называют множество G с заданной на нем бинарной операцией •, если:

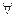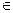а) Операция • ассоциативна, то есть a,b,c G выполняется (a•b)•c=a•(b•c);

б) a•e=e•a=a (Если групповая операция называется сложением, то e называют нулевым элементом, если операция – умножение, то e называют единичным элементом.);

в) (Если групповая операция называется сложением, то x´ называют противоположным к x элементом, если операция – умножение, то обратным элементом.);

Если операция группы <G,•> коммутативна (то есть ), то группа называется коммутативной, или абелевой.

Утверждение 1

< Z_m , +(mod m)> — абелева группа.

Доказательство

Докажем, что Z_m вместе с операцией сложения по модулю m образуют абелеву группу. Действительно, операция сложения не выводит за пределы множества целых чисел, а Z_m покрывает своими вычетами всё Z, поэтому можно сказать, что операция +(mod m) задана на Z_m. Ассоциативность операции +(mod m) следует из ассоциативности сложения, в качестве нулевого элемента выступает «0», а в качестве противоположного к a выступает m—a. Коммутативность групповой операции следует из коммутативности сложения.



Более того, как нетрудно показать, любая полная система вычетов вместе с операцией сложения по модулю m образует абелеву группу.

Утверждение 2

<U_m, · (mod m)> — абелева группа.

Доказательство

Докажем, что умножение по модулю m задано на приведенной системе вычетов по модулю m. Действительно, U_m покрывает своими вычетами всё Z кроме тех чисел, которые имеют с m общие нетривиальные делители. Результат умножения двух чисел, каждое из которых взаимно просто с m, также будет взаимно просто с m. Согласно свойству сравнений №15, числа одного и того же класса по модулю m имеют с модулем m один и тот же наибольший общий делитель. Это значит, что операция умножения по модулю m не выводит за пределы U_m, а значит задана на U_m.

Ассоциативность и коммутативность операции · (mod m) следует из ассоциативности и коммутативности умножения, единичным элементом является «1». Каждый элемент множества U_m имеет обратный согласно теореме обратимости в силу того, что все элементы U_m взаимно просты с m.



Из курса алгебры мы знаем, что группа, содержащая конечное число элементов, называется конечной группой.

Кольцом называют непустое множество K вместе с заданными на нем бинарными операциями + и ∙ , если:

а) <K,+> — абелева группа;

б) Операция ∙ ассоциативна;

в) Операция ∙ дистрибутивна относительно + (то есть a∙(b+c)=(a∙b)+(a∙c), (a+b)∙c=(a∙c)+(b∙c));

Кольцо <K,+,∙> называют коммутативным, если операция ∙ коммутативна.

Кольцо <K,+,∙> называют кольцом с единицей, если x∙e=e∙x=x.

Полем называют коммутативное кольцо с единицей <P,+, ∙ >, в котором каждый ненулевой элемент обратим по операции ∙ .

Утверждение

<Z_p,+(mod p), ∙ (mod p)> — поле, если p – простое число.

Доказательство:

Согласно утверждению 1, <Z_p,+(mod p)> - абелева группа, причем в качестве нулевого элемента выступает 0 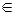Z_p. Поскольку Z_p покрывает своими вычетами всё множество целых чисел, а операция умножения не выводит целые числа за пределы Z, то и операция умножения по модулю p не выводит за пределы Z_p. То есть операция ∙ (mod p) задана на Z_p.

Ассоциативность и коммутативность операции ∙ (mod p) следует из аналогичных свойств операции умножения, дистрибутивность умножения по модулю p относительно сложения по модулю p следует из дистрибутивности умножения относительно сложения.

В качестве единицы по операции ∙ (mod p) выступает 1 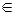Z_p.

Итак, <Z_p,+(mod p), ∙ (mod p)> — коммутативное кольцо с единицей. А поскольку в силу простоты p все элементы, кроме нулевого, взаимно просты с модулем p, то, по теореме обратимости, обратим по операции ∙ (mod p).

Следовательно, по определению поля, <Z_p,+(mod p),∙(mod p)> — поле.

□

Из курса алгебры мы знаем, что поле, содержащее конечное число элементов, называется конечным полем. Конечные поля называются полями Галуа по имени их первооткрывателя, Эвариста Галуа.

Число элементов в поле называется его мощностью. Все поля одинаковой мощности изоморфны друг другу. Таким образом, любое поле, мощность которого есть простое число, изоморфно <Z_p,+(mod p),∙(mod p)> для подходящего p.

Поле <Z_p,+(mod p),∙(mod p)> иначе обозначается GF(p), то есть поле Галуа мощности p.

Кроме полей GF(p) существуют поля составной мощности. Различают GF(2^α), GF(p^α) (где p – простое число, не равное 2 ). В настоящей главе мы будем рассматривать поля GF(p), получим для таких полей некоторые результаты, а затем, во второй главе, обобщим их и на другие конечные поля.