VII. Элементы теории игр

1. Экономические задачи, приводящие к игровым моделям. Общие понятия теории игр. Чистые, смешанные, оптимальные стратегии. Седловая точка.

2. Решение игр в смешанных стратегиях. Связь матричных игр с задачами линейного программирования.

Литература: 3(гл. 13), 4(гл. 12).

введение

Возникшие новые пути приложения математики повлекли за собой глубокие изменения в самой математической науке. Они не только вызвали к жизни новые значительные направления теоретической математики (из которых такие, как теория игр или теория информации, заняли уже положение самостоятельных математических наук), но и способствовали изменению установившихся взглядов на ранее сложившиеся разделы. Наиболее существенным здесь является то, что некоторые разделы математики представляются нам теперь гораздо более содержательными и важными, чем это казалось математикам ХІХ века или первой половины ХХ века (как это произошло, например, с алгеброй).

Если начиная с XVII века главенствующее положение в математике занимало изучение функций непрерывно меняющегося аргумента, являющееся основой всех приложений математики к физике и к технике, то сегодня можно говорить о возрождении интереса к “конечной” математике. При этом возникли новые подходы к этой ветви математики, идущие в основном от математической логики.

В настоящее время наблюдается “математизация” целого ряда дисциплин, ранее далеких от всякого влияния математических методов – лингвистики, экономической теории, медицины, педагогики, психологии, теории искусства.

Применение математики в экономических исследованиях дает возможность углубить и уточнить представление о качественной стороне закономерностей, о существе тех предметов и явлений, которые подвергаются исследованию.

Остановимся на некоторых, наиболее важных направлениях экономико-математических исследований.

1. Использование математических методов при установлении экономически обоснованных цен, при разработке экономических критериев рентабельности, ориентируясь на которые отдельные государственные и частные предприятия могли бы в полной мере осуществлять хозяйственный расчет и сочетать свои и государственные интересы.

2. Разработка межотраслевых балансов производства и распределения. У нас имеется некоторый опыт балансовых построений. Однако пока еще не создана экономико-математическая модель, которая базировалась бы на системе математических уравнений и неравенств и давала возможность решать на оптимум различные экономические задачи. Построение такой модели обеспечит решение экстремальных задач на минимум затрат общественного труда и на максимально возможный уровень материальной обеспеченности членов общества.

3. Обеспечение рационального размещения производства при планировании работы транспорта. К числу экономических проблем такого рода относится распределение судов флота между определенными участками водных путей сообщения, наилучшее закрепление самолетов за определенными линиями, оптимальная эксплуатация различных средств транспорта на перевозках различных видов грузов, выбор рациональной схемы движения порожнего состава и др.

4. Решение разнообразных технико-экономических задач – задач на нахождение оптимального плана использования производственных мощностей (например, загрузки станков), на рациональный раскрой материалов, на наивыгоднейшее расположение хозяйственных объектов (складов, магазинов и пр.), на оптимальный состав химических и иных промышленных смесей, на определение наилучших пищевых наборов и рационов и т.д.

5. Математика перестала быть вспомогательной наукой, теперь она – мощный аппарат производства, профилирующая дисциплина в экономических исследованиях. Отметим особую роль электронно-вычислительной техники при внедрении математики в экономику. С появлением машин от математиков потребовалось создание новых, более мощных вычислительных методов, были поставлены новые вычислительные задачи.

Создание электронных вычислительных машин произвело революцию в области вычислительной математики и привело к возникновению нового раздела современной математики – математического программирования. К задачам математического программирования относятся задачи оптимизации, которые, как правило, не решаются классическими приемами. Это, прежде всего, задачи математической экономики. Они возникают в тех случаях, когда дефицитные ресурсы – люди, машины, сырье – следует распределить так, чтобы произвести необходимое количество продуктов и расходы при этом были минимальными (или доход максимальный). Огромный интерес к этим задачам объясняется прежде всего тем, что они встречаются не только в теоретической экономике, но и в практике производства, торговли, управления и в военном деле.

Точная экономическая наука особенно нужна теперь, когда непрерывно развивается экономика, и очень усложнились хозяйственные связи. С математической точки зрения методы математического программирования применимы лишь к тем явлениям и процессам, которые выражаются положительными величинами. Величины, характеризующие экономические явления, этим условиям, как правило, удовлетворяют. Математическое программирование можно применять к таким задачам, при решении которых оптимальный результат достигается лишь в виде сформулированных целей и при вполне определенных ограничениях, вытекающих из наличия средств.

Следовательно, для любых задач математического программирования характерны три следующих момента:

ü наличие системы взаимозависимых факторов;

ü строго определенный критерий оптимальности;

ü точная формулировка условий, ограничивающих использование наличных ресурсов или факторов.

Решение задачи достигается применением определенной математической процедуры, которая заключается в последовательном приближении рациональных вариантов, соответствующих выбранным факторам, к оптимальному плану. Сделаем несколько замечаний по постановке задач математического программирования, они затрагивают ряд организационных моментов.

Математический анализ применяется не к реальным явлениям, а к некоторым математическим моделям этих явлений. Такие абстрактные модели, естественно, охватывают не все, а лишь важнейшие для данной задачи стороны явления. Наиболее квалифицированная и ответственная работа при постановке задачи заключается в выборе характеристики явления – в решении, какими характеристиками пренебречь и какие учесть. При выборе переменных желательно обеспечить возможно более простой вид условий и критерия оптимальности. При построении математических моделей исследуемых явлений, особенно в тех случаях, когда эти явления изучаются впервые, не всегда удается сразу сформулировать и записать все условия. Некоторые факторы и ограничения, представляющиеся естественными, предполагаются само собой подразумевающимися и специально не оговариваются. Так, известны, например, случаи, когда при решении задачи о диете с минимальной стоимостью не были учтены вкусовые характеристики диеты. В результате были получены совершенно не съедобные рационы. Иногда встречаются случаи, когда решение, оптимальное с формально-математических позиций, неприемлемо для производства как не удовлетворяющее экономическим, технологическим и другим требованиям, предъявляемым к данному производственному процессу.

Следовательно, применение методов математического программирования может принести пользу тогда, когда условия задачи учитывают экономические, технологические и другие особенности процесса. Поэтому постановку серьезных задач математического программирования целесообразно проводить специалистам прикладных наук совместно с математиками.

Одним из важнейших разделов современной математики является теория игр. Она занимается изучением конфликтных ситуаций. Теория игр вызвана к жизни практическими потребностями в моделях и методах экономического и военного планирования. Эта теория развивалась независимо от математического программирования, пока в 50-х годах не была обнаружена замечательная связь между линейным программированием и теорией игр. Переплетение и взаимное проникновение этих дисциплин оказались полезными для каждой из них. Вычислительные приемы линейного программирования обогатились методами решения игр (итеративными) и наоборот.

Классификация задач математического программирования.

Задачи и методы математического программирования можно классифицировать по различным признакам. Полезно знать хотя бы одну из существующих классификаций, которая, прежде всего, выявляет в задаче наличие элемента случайности или его отсутствие.

Задачи математического программирования могут быть подразделены на два больших класса: детермированные задачи и стохастические (вероятностные).

Детермированными называются такие задачи, в которых критерий оптимальности не является случайной функцией параметров. В таких задачах почти с достоверностью можно описать необходимые условия осуществления действий (ограничения) и исходы этих действий. Параметры в этих задачах также не являются случайными величинами.

Стохастическими называются задачи, которые включают в себя неопределенность. Критерий оптимальности в таких задачах является некоторой характеристикой случайной функции параметров задачи. Неопределенность может возникнуть во многих случаях. Результаты некоторого действия могут зависеть от таких факторов, как погода, задержка автотранспорта, уровень занятости, повышение или падение покупательского спроса.

Класс детерминированных задач подразделяется на линейные задачи и нелинейные. Стохастические задачи можно тоже разбить на две группы, каждая из которых в свою очередь подразделяется на подгруппы.

В тех случаях, когда целевая функция (или критерий оптимальности) выражена линейно через исходные факторы, а условия, ограничивающие использование наличных ресурсов или факторов, записываются в виде линейных неравенств или равенств относительно искомых величин, мы приходим к задаче линейного программирования. Следует заметить, что в рамки линейного программирования укладывается огромное количество самых разнообразных задач перспективного и оперативного планирования хозяйства, управления различного рода процессами.

Почти параллельно с линейным программированием развивается нелинейное, представляющее значительно более сложную математическую задачу. В настоящее время еще нельзя говорить о законченной теории нелинейного программирования, но разработка ее осуществляется очень интенсивно. Из нелинейных задач выделяются задачи выпуклого программирования.

К задачам выпуклого программирования относятся задачи, у которых показатели качества и область определения оптимизируемой функции предполагаются выпуклыми. Между линейным и выпуклым программированием существует тесная связь. Любая выпуклая задача может быть сведена к задаче линейного программирования.

Среди задач выпуклого программирования подробнее других исследованы задачи квадратичного программирования. Для них характерно то, что функции цели представляют собой квадратичную форму, а ограничения линейны. Уже сейчас имеются методы для решения задач квадратичного программирования и более общего типа. Современная математическая наука располагает целым арсеналом методов, позволяющих решить задачу оптимального управления. Среди них особое место занимает метод динамического программирования. Специфика этого метода заключается в том, что для отыскания этого оптимального управления планируемая операции разделяется на ряд последовательных “шагов” или “этапов”. Соответственно и сам процесс планирования становится “многошаговым” и развивается последовательно от этапа к этапу, причем каждый раз оптимизируется управление только на одном этапе.

Если мы рассматриваем экономико-математическую модель не как застывшую задачу, а берем ее в динамике, желая найти решение на несколько периодов времени, то, естественно, возникает динамическая задача, и имеет смысл говорить о динамическом программировании. Динамические модели наиболее интересны для плановых расчетов, если плановую экономику рассматривать с точки зрения управляемых систем, а также при решении задач раскроя и др. задач.

Исследование задач, у которых коэффициенты ограничений, коэффициенты линейной формы, а также правые части ограничений зависят от параметра, составляет предмет параметрического программирования. В этой области еще много нерешенных проблем. Рассмотрен детально лишь частный случай, когда от параметра зависят коэффициенты линейной формы и правой части ограничений.

Целочисленными принято называть такие задачи линейного программирования, в которых переменные должны принимать лишь целые неотрицательные значения из допустимой области. Подобные задачи могут возникнуть различными путями. Прежде всего, существуют задачи, которые формально не относятся к целочисленным, но решения их при целых исходных данных автоматически получаются целочисленными. Такова известная транспортная задача и ее различные варианты.

Наиболее естественным источником целочисленных задач являются важнейшие в прикладном отношении задачи линейного программирования, в которых требуется составить план использования неделимых ресурсов (например, холодильников).

Целочисленное программирование приобретает особый интерес, потому что многие нелинейные выпуклые задачи математического программирования могут быть сведены к задачам линейного программирования с дополнительным требованием целочисленности решения.

Мы уже отмечали, что задачи, в которых нельзя пренебречь ошибками эксперимента, называются стохастическими. Это означает, что в такой задаче коэффициенты целевой функции и системы ограничений нельзя установить однозначно. А это приводит к тому, что с изменением одного или несколько коэффициентов изменяются оптимальные значения входящих в задачу параметров. Стандартные методы решения дают оптимальное решение только для определенного набора значений параметров, поэтому их использование здесь исключается.

Если для случайных величин, фигурирующих в задаче, известно вероятностное распределение, то говорят, что задача решается в условиях риска. Если вероятностное распределение неизвестно, то имеем задачу в условиях неопределенности. Примером задачи в условиях риска являются задачи управления запасами, а задачи специального стохастического анализа могут оказаться в условиях неопределенности. Из всех разделов математического программирования стохастическое наименее разработано.

2. Методические рекомендации

2.1 Постановка задач линейного программирования

Промышленное производство, ресурсы в экономике, напряжение сил в военных действиях – это комплексы многочисленных взаимоувязанных процессов. В управлении этими совершенно различными явлениями можно выделить существенные черты сходства. При описании задач оптимизации оказывается, что задачи, различные по содержанию, могут быть представлены однотипными математическими моделями.

Наиболее простой и изученной является модель линейного программирования. Она содержит в себе три основных момента:

§ набор неотрицательных переменных, характеризующих изучаемый процесс или явление;

§ соотношения, устанавливающие связь между переменными (ограничения) и отражающие требования задачи;

§ критерий оптимальности (функцию цели).

В задачах линейного программирования ограничения представляют собой систему линейных неравенств и уравнений, выражающих условие материального баланса (т.е. чтобы расход любого вида сырья не превышал имеющегося запаса данного сырья и т.д.). Функция цели тоже имеет линейный вид.

Прежде чем перейти к рассмотрению общей задачи линейного программирования, разберем несколько примеров.

Задача производственного планирования.Предположим, что на некотором предприятии имеется видов сырья для производства видов изделий. Известны нормы расхода каждого вида сырья на единицу каждого вида изделия. Кроме того, известны запасы каждого вида сырья и доход предприятия от реализации единицы изделий каждого вида.

Задача производственного планирования состоит в определении количества изделий каждого вида, которое должно производить предприятие, чтобы расход имеющегося сырья не превышал его запасы, а доход предприятия был бы как можно больше, т.е. достигал максимума.

Примем следующие обозначения:

–	число ресурсов (число видов сырья);
–	число видов изделий;
–	запасы сырья -го вида ;
–	доход от продажи -го изделия ;
–	норма расхода сырья -го вида на производство одного изделия -го вида

Очень удобной формой записи условия задачи является таблица следующего вида.

Таблица 1

Виды сырья	Норма расхода 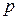-го сырья на -ое изделий	Запасы сырья
В и д ы и з д е л и й
1	2	3	…
				…
				…
…	…	…	…	…	…	…
				…
Доход				…

В качестве неизвестных в задачах линейного программирования берут те величины, которые нужно определить. В данной задаче:

–	количество изделий 1-го вида, которое должно произвести предприятие;
–	количество изделий 2-го вида;
–	количество изделий 3-го вида;
………………………………………
–	количество изделий -го вида.

Составим ограничения.

Если на одно изделие I вида расходуется первого вида сырья, то на все изделия I вида сырья пойдет . На все изделия II вида этого же сырья потребуется (так как на одно изделие идет , а всего изделий ). На все изделия III вида необходимо сырья I вида и т.д., и, наконец, для производства последнего вида изделий сырья I вида потребуется . Всего сырья I вида будет израсходовано:

+ + + … +

– эта величина складывается из расходов сырья I вида по каждому виду изделия. А так как запасы ограничены, то эта сумма не должна превышать величину запаса по этому виду сырья (т.е. должна быть меньше ее или равна ей):

+ + … + .

Аналогично по второму виду сырья: следует учесть расходы этого сырья по всем изделиям каждого вида, а затем найти суммарный расход, и этот расход сырья II вида не должен превосходить запасы сырья этого вида. Тем самым получим второе ограничение

+ + … + .

Проведя подобные рассуждения для всех видов сырья, получим систему ограничений, описывающую данную задачу:

+ + … + ,

+ + … + ,

……………………………………..

+ + … + .

Поскольку количество изделий любого вида не может быть отрицательным, требуем, чтобы все введенные неизвестные были больше нуля или, в крайнем случае, равны нулю.

Доход, получаемый от производства всех изделий первого вида, составляет ; от производства изделий второго вида – и т.д. и от производства изделий -го вида он равен . Общий доход выразится в виде суммы этих величин.

Таким образом, задача заключается в нахождении таких переменных , которые удовлетворяют условиям

, , … , + + … + , + + … + , ……………………………………… + + … + .

и обращают функцию дохода 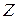= + +…+ в максимум.

Транспортная задача.Пусть в пунктах производится некоторый однородный продукт, причем объем производства (мощность) в каждом пункте известен. Этот продукт потребляется в пунктах , при этом известен объем потребления (спрос) для каждого пункта. Предполагается, что суммарная мощность совпадает с суммарным спросом. Допустим, что транспортировка возможна из любого пункта производства в каждый пункт потребления, причем транспортные издержки, приходящиеся на единицу продукта, считаются заданными. (Под транспортными издержками понимают время перевоза, расстояние, стоимость).

Транспортная задача заключается в распределении производимого продукта так, чтобы спрос был удовлетворен и суммарные транспортные издержки были минимальными.

Введем обозначения:

–	число поставщиков;
–	число потребителей;
–	общее количество единиц продукта, необходимое -му потребителю ;
–	общее количество единиц продукта, выделяемое для перевозки -м поставщиком ;
–	транспортные издержки, приходящиеся на единицу продукта, при перевозке из -го пункта в -ый пункт , .

Составим таблицу. Она даст нам более четкое представление о задаче.

Таблица 2

Пункты производства	Объем производства	Транспортные издержки на одно изделие
Пункты потребления и спрос
		……
				…
				…
…	…	…	…	…	…
				…

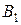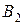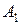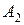Особенностью транспортной задачи является наличие большого числа переменных, поэтому имеет смысл ввести двойные индексы. Обозначим через – количество продукта, перевозимого из первого пункта производства в первый пункт потребления, через – количество продукта, перевозимого из первого пункта производства во второй пункт потребления, и т.д., – количество продукта, перевозимого из 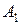в (первый индекс указывает номер пункта производства, второй – номер пункта потребления). Аналогично из второго пункта производства мы вывезем

–	в первый пункт потребления;
–	во второй пункт потребления;
………………………………………..
–	в -ый пункт потребления.

Подобно предыдущему, для всех пунктов производства введем свои неизвестные. В частности, для последнего

– из -го пункта в первый;

– из -го пункта во второй;

……………………………………

– из -го пункта в -ый.

При этом по-прежнему первый индекс у неизвестного указывает номер пункта отправки, а второй – номер пункта потребления. То есть означает количество продукции, перевозимой из пятого пункта производства в седьмой пункт потребления.

Составим ограничения. Прежде всего учтем, что общий спрос равен общему предложению, т.е.

.

Исходя из введенных обозначений, получим, что величина выражает собой не что иное, как количество единиц продукта, вывезенного из первого пункта производства во все пункты потребления. А так как продукт, имеющийся в этом пункте, должен быть распределен полностью без остатка, то, очевидно, эта сумма должна равняться имеющемуся запасу продукта, т.е.

.

Рассуждая аналогично предыдущему, получим, что величина характеризует количество единиц продукта, перевозимого из второго пункта производства во все пункты потребления и т.д.; величина указывает, сколько единиц продукта вывезено из -го пункта производства во все пункты потребления. И эти величины также должны согласовываться с мощностью соответствующего поставщика.

В итоге получим систему, отражающую интересы поставщиков

(1)

Однако эта система никак не учитывает интересы потребителей, ведь совсем не безразлично, сколько куда везти. Необходимо удовлетворить спрос потребителей. С этой целью будем подсчитывать, сколько в какой пункт мы везем от всех поставщиков. Так, в первый пункт мы везем от первого поставщика , от второго – и т.д. от -го – . Количество продукта, завезенного от всех поставщиков, должно совпадать с величиной спроса – объема потребления. Подобно этому, во второй пункт потребления мы перевозим из первого пункта производства, – из второго пункта производства и т.д. – из -го пункта производства. Сумма этих величин должна равняться объему потребления во втором пункте. Такого рода рассуждения приведут в тому, что в -ый пункт назначения мы перевозим величину из первого пункта производства, – из второго пункта и т.д. – из -го пункта.

Таким образом, нами получена еще одна система, которая отражает интересы потребителей

(2)

Естественно, что все введенные нами неизвестные не могут принимать отрицательных значений, т.е. .

Общие транспортные издержки будут складываться из затрат, возникающих при перевозке из каждого пункта производства в каждый пункт потребления необходимого количества единиц продукта. Суммарные издержки могут быть выражены с помощью функции цели следующего вида:

Итак, наша задача заключается в нахождении таких неотрицательных величин , которые удовлетворяли бы системам (1) и (2), а целевая функция 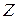была бы минимальной.