D) Решение дифференциального уравнения , описывающего зависимость выходного напряжения от входного сигнала цепи, с входным сигналом заданным дифференциалом от функции Гаусса
Для начала зададим параметры входного сигнала, и сам сигнал:
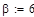 |
| - коэффициент функции гаусса |
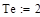 - длительность сигнала - длительность сигнала |
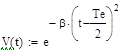 - функция гаусса - функция гаусса |
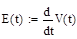 - аналитическое выражение нашего входного сигнала - аналитическое выражение нашего входного сигнала |
Затем запишем аналитическое выражение зависимости выходного напряжения в нашей RL цепи от входного сигнала. Найдем изменение выходного напряжения, и пронаблюдаем ее на графике.
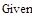 |
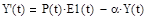 - дифференциальное уравнение, описывающее процесс изменения выходного напряжения в цепи (4.1) - дифференциальное уравнение, описывающее процесс изменения выходного напряжения в цепи (4.1) |
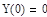 - начальное условие - начальное условие |
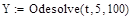 - нахождение изменения выходного напряжения - нахождение изменения выходного напряжения |
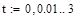 |
Где Е1(t) является дифференциалом от входного радиосигнала, и имеет вид:
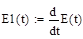 |
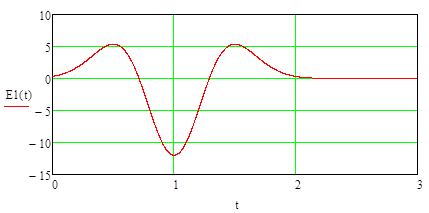 |
Рисунок 4. График производной от входного сигнала.
Теперь представим график изменения выходного напряжения:
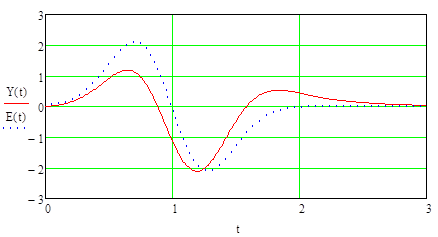 |
Рисунок 5. График входного и выходного сигналов цепи.
Вывод: в катушке индуктивности, включенной в цепь переменного тока, создается сопротивление прохождению тока. На рисунке (5)мы можем наблюдать, что происходит задержка по времени выходного сигнала из за индуктивности, и падения напряжения из за сопротивления. При увеличении α выходной сигнал начинает приближаться к дифференциалу входного (дифференцируется), а при уменьшении к самому входному сигналу.
Основные Выводы.
1)В ходе данной курсовой работы мы получили навыки для описания математических моделей процессов происходящих в электрических цепях на основе, дифференциальных уравнений и законов физики. Было составлено дифференциальное уравнение, описывающее процессы, происходящие в электрической цепи. Были найдены напряжения на определенных элементах цепи, и установлено влияние на эти напряжения входного ЭДС.
2)С помощью системы математического моделирования MathCAD, данное дифференциальное уравнение было решено при определённых начальных условиях. С помощью решения данного дифференциального уравнения, была установлена зависимость выходного сигнала от входного. Эта зависимость была изображена на графиках.
3) В ходе работы мы отмоделировали:
A) Переходные процессы в цепи.
На рисунке (2) мы видим, как индуктивность реагирует на единичный скачек напряжения. Напряжение переходит в стабильное состояние (становится равным нулю). Мы наблюдаем постоянное выходное напряжение. Вся накопленная в соленоиде энергия расходуется на нагрев сопротивления. Напряжение на катушке при постоянном входном сигнале стремится к нулю, так как сопротивление идеального соленоида равно нулю и исходя из формулы (1.2). Напряжение накатушке при постоянном токе равно нулю.
