Условная вероятность рассчитывается по формуле
Р(А|В) = 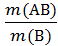 .
.
Делением числителя и знаменателя на общее число исходов N находим
Р(А|В) = 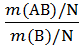 =
= 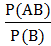 .
.
Эта формула при Р(В) ¹ 0 принимается за определение вероятности события А при условии, что произошло событие В.
Из этой формулы следуют такие свойства условной вероятности:
1. Р(А|А) = 1.
2. В Ì А Þ Р(А|В) = 1.
3. Р(Ω|В) = 1, Р(∅|В) = 0 при В ≠ ∅.
4. Для несовместных событий 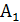 и
и 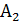
Р( 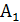 +
+ 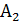 |В) = Р(
|В) = Р( 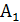 |В) + Р(
|В) + Р( 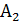 |В).
|В).
5. Ввиду коммутативности произведения событий АВ=ВА находим
| ∥ |
Р(ВА)= Р(В|А) Р(А).
Пример. Из урны с 4-мя белыми и 6-ю черными шарами последовательно извлекаются два шара без возвращения. Какова вероятность того, что первый шар белый, а второй - черный (событие А).
Решение данной задачи по классической схеме дает следующий результат. Всего в эксперименте N = 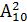 = 10·9 = 90 исходов по числу упорядоченных пар, образуемых из 10 шаров. Благоприятных исходов m(А)=4·6=24 поскольку белый шар может быть выбран 4-мя способами, каждый из которых может комбинировать с любым из 6-ти способов выбора черного шара. Убедиться в этом, как и ранее помогает числовая таблица, в которой белые и черные шары условно перенумерованы, а комбинации их номеров оформлены с помощью слеша.
= 10·9 = 90 исходов по числу упорядоченных пар, образуемых из 10 шаров. Благоприятных исходов m(А)=4·6=24 поскольку белый шар может быть выбран 4-мя способами, каждый из которых может комбинировать с любым из 6-ти способов выбора черного шара. Убедиться в этом, как и ранее помогает числовая таблица, в которой белые и черные шары условно перенумерованы, а комбинации их номеров оформлены с помощью слеша.
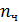 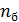 | 1 2 3 4 5 6 |
| 1\1 1\2 1\31\4 1\5 1\6 2\1 2\2 2\3 2\4 2\5 2\6 3\1 3\2 3\3 3\4 3\5 3\6 4\1 4\24\3 4\4 4\5 4\6 |
В итоге находим искомую вероятность
Р(А)= 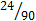 =
= 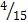 .
.
Решим эту же задачу с помощью условной вероятности. Если за событие Б принять извлечение белого шара, а Ч - черного, то событие А можно представить в виде А=БЧ, и тогда следуя формальной схеме условной вероятности получим расчетную формулу Р(А)=Р(БЧ)=Р(Б|Ч)Р(Ч), которая предполагает извлечение первым черного шара, что противоречит постановке задачи. Однако это противоречие мнимое и преодолеть его помогает свойство коммутативности произведения случайных событий, используя которое находим Р(А)=Р(БЧ)= Р(ЧБ)=Р(Ч|Б)Р(Б). Теперь расчетная формула полностью соответствует схеме выбора шаров.
Поскольку из урны с 10-ю шарами первым извлекается белый шар, то Р(Б)= 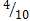 =
= 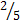 . Черный шар извлекается из урны уже с 9-ю шарами, из которых 6 черных и потому Р(Ч|Б)=
. Черный шар извлекается из урны уже с 9-ю шарами, из которых 6 черных и потому Р(Ч|Б)= 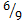 =
= 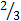 . В итоге получаем Р(А)=
. В итоге получаем Р(А)= 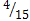 , что находится в полном согласии с классической вероятностью. Данный пример показывает, что использование условной вероятности требует грамотного применения соответствующей схемы на основе содержательного анализа исходных данных, тогда как ее формальное применение может завести в тупик.
, что находится в полном согласии с классической вероятностью. Данный пример показывает, что использование условной вероятности требует грамотного применения соответствующей схемы на основе содержательного анализа исходных данных, тогда как ее формальное применение может завести в тупик.
Наряду с несовместностью случайных событий важным понятием является их независимость, определяемая как отсутствие влияния одного события на вероятность другого события.
Событие А не зависит от события В, если
Р(А|В)=Р(А),
