Обработка результатов физического эксперимента на примере определения ускорения свободного падения с помощью математического маятника

Студент_____________________________группа ___________________

Допуск________________________________Выполнение____________________Защита___________________

Цель работы: получение и закрепление навыков обработки результатов прямых, косвенных и совместных

измерений.

Приборы и материалы: математический маятник, измерительная линейка, секундомер.

Упражнение 1.Порядок обработки прямых измерений. Определение периода колебаний математического маятника.

1. Получите у преподавателя значения длины нити математического маятника 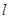и проведите 10 замеров периода колебаний маятника. Результаты запишите в черновик.

2. Из 10 полученных замеров, выберите пять наиболее близких друг к другу по величине и запишите их в таблицу 1.

Таблица 1

Nизм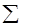

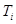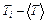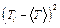3. Просуммируйте все значения 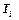и данную сумму занесите в соответствующую графу 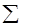. Используя значение этой суммы, по формуле 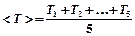найдите среднее значение периода колебаний математического маятника.

=

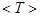4. Зная 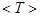, заполните окончательно таблицу 1.

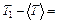
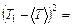
5. Используя данные этой таблицы, найдите дисперсию среднего значение периода колебаний маятника по формуле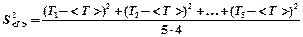

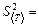
6. Найдите среднеквадратичное отклонение среднего значения по формуле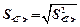

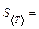
7. Результат измерения периода колебаний запишите в виде: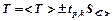

где для вероятности 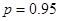и числа степеней свободы 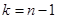, значение параметра Стьюдента 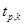= 2.8

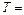
Упражнение 2.Обработка результатов косвенных измерений. Определение ускорения свободного падения

1. Запишите в табл. 2 пять значений периода колебаний маятника из упражнении 1.

Таблица 2

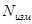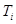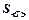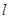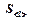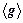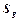2. По формуле 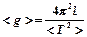вычислите среднее значение ускорения.

3. Вычислите дисперсию ускорения свободного падения по формуле:

;

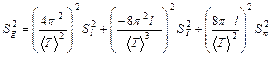В качестве погрешности в определении длины нити математического маятника 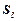возьмите квадрат приборной погрешности (в качестве приборной погрешности принимается величина, равная половине цены деления шкалы прибора).

=

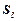В качестве погрешности числа 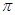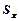возьмите табличную погрешность (в качестве табличной погрешности принимается величина, равная половине единицы последнего разряда округлённой табличной величины).

=

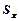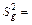
Величину 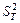рассчитайте по формуле 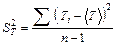, где n – число измерений.

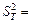
4. Найдите среднеквадратичное отклонение ускорения по формуле: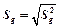

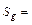
5. Результат измерения ускорения запишите в виде: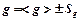

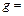
Упражнение 3.Порядок обработки совместных измерений. Определение ускорения свободного падения

В этом упражнении необходимо определить ускорение свободного падения из совместных измерений длины математического маятника и его периода колебаний.

Период колебаний математического маятника вычисляется по формуле .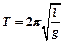

Для того, чтобы воспользоваться методом обработки совместных измерений для зависимости 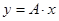введем следующие обозначения: ; ; .

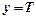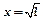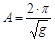Таким образом, зная экспериментальную зависимость 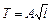, можем вычислить коэффициент .

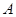Затем из соотношения 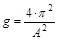определим ускорение свободного падения.

1. Уменьшая первоначальную длину маятника (из упражнения 1) каждый раз на 5 см, проведите по три замера на каждой длине и среднее из этих трёх значений запишите в табл. 3 (графы 2 и 3). Всего необходимо провести измерения при пяти различных длинах математического маятника.

2. В соответствии с вышеприведенными обозначениями заполните графы 4 и 5.

Таблица 3

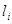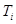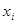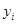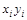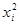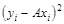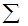3. Проведите соответствующие вычисления и заполните графы 6 и 7 табл. 3. В графу 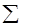вносится сумма соответствующих колонок.

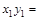
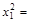
4. По формуле 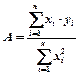вычислите значение параметр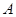а . А=

5. Проведите соответствующие расчеты и заполните графу 8.

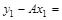
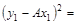
Далее по формуле 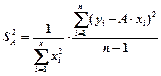вычислите дисперсию параметра А .

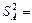
6. По формуле 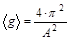вычислите среднее значение ускорения свободного падения.

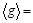
7. По формуле 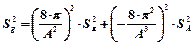вычислите среднеквадратичное отклонение среднего значения ускорения свободного падения.

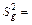
8. Окончательный результат запишите в виде .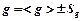

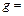
9. В координатах 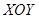постройте график зависимости 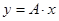, там же нанесите звездочками экспериментальные данные . (в качестве возьмите 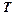, в качестве 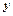возьмите ).

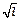Для проверки соответствия зависимости 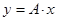экспериментальным данным примените 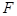- критерий (критерий Фишера). Для этом вычислите следующее соотношение

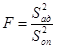, где 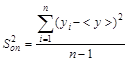- дисперсия опыта (или дисперсия воспроизводимости) с числом степеней свободы равным n - 1, где n - число прямых измерений величины 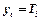. Значения 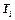возьмите из первого упражнения (n = 5),

а 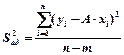- дисперсия адекватности, где 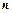- число измерений ( 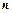= 5), а 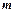- число коэффициентов в уравнении 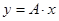, ( 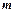= 1).

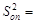
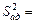
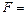
Далее проверьте двухстороннее неравенство 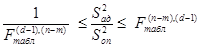, где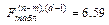

(В том случае, когда 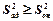, достаточно производить одностороннюю оценку, т.е. ).

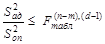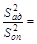
Если окажется, что 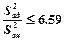, то с вероятностью, равной 95 %, можно утверждать, что наше предположение о линейной зависимости между величинам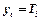и и 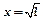действительно описывается зависимостью .

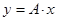10. Сделайте окончательный вывод.

Пример оформления лабораторной работы

ЛАБОРАТОРНАЯ РАБОТА 0-1: