Пример выполнения работы
Найти решение методом Гаусса системы  , где
, где

Выполняем расчеты с помощью МК.
1. Сначала выбираем максимальный по модулю элемент среди элементов первого столбца матрицы A. Он равен 8,30 и находится в первом уравнении. Поэтому нет необходимости в перестановке строк.
2. Заносим коэффициенты системы в первые 4 строки бланка расчета в столбцах, отмеченных буквами  (табл. 1.2).
(табл. 1.2).
3. Суммируем элементы в каждой строке и записываем сумму в последний, контрольный столбец, обозначенный  .
.
4. Заполняем далее столбец  (m – номер уравнения, m=2,3,4). Во второй – четвертой строках этого столбца записываем числа, которые вычисляются по формулам (1.5):
(m – номер уравнения, m=2,3,4). Во второй – четвертой строках этого столбца записываем числа, которые вычисляются по формулам (1.5):

Первые 4 строки бланка заполнены полностью (табл. 1.2).
5. Для получения следующих трех строк применим формулы (1.6). Так элементы первой из этих строк будут равны

Для выполнения контроля суммируем элементы этой строки (кроме последнего). Получаем
2,311253 + 0,598314 + 6,484097 – 5,644710 = 3,754254.
Сравниваем этот результат с  . Отличие наблюдается лишь в последнем десятичном знаке, значит наши вычисления верны. Аналогично находим и контролируем элементы остальных строк. Первый цикл закончен. Для выполнения второго цикла необходимо выбрать новую ведущую строку по коэффициентам при
. Отличие наблюдается лишь в последнем десятичном знаке, значит наши вычисления верны. Аналогично находим и контролируем элементы остальных строк. Первый цикл закончен. Для выполнения второго цикла необходимо выбрать новую ведущую строку по коэффициентам при 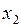 . Это будет уже вторая строка (
. Это будет уже вторая строка (  ). Переставляем ее на место первой и повторяем уже проделанные расчеты; и так до окончания прямого хода.
). Переставляем ее на место первой и повторяем уже проделанные расчеты; и так до окончания прямого хода.
Таблица 1.2
Расчетный бланк метода Гаусса
| Номер Цикла | m |  |  |  |  |  |  |  |
| k=1 | 0,266265 0,472289 0,454217 | 8,30 2,21 3,92 3,77 | 3,12 3,15 8,45 7,71 | 4,10 1,69 7,28 8,04 | 1,90 6,99 2,46 2,28 | – 10,15 – 8,35 12,21 14,95 | 7,27 5,69 34,32 36,75 | |
| Конеццикла | 2,319253 6,976458 6,292844 | 0,598314 5,343615 6,177711 | 6,484097 1,562651 1,416988 | – 5,647410 17,003734 19,560300 | 3,754254 30,886458 33,447843 | |||
 |  |  |  |  |  |  | ||
| k=2 | 0,332440 0,902011 | 6,976458 2,319253 6,292844 | 5,343615 0,598314 6,177711 | 1,562651 6,484097 1,416988 | 17,003734 – 5,647410 19,560300 | 30,886458 3,754254 33,447843 | ||
| Конеццикла | – 1,178117 1,357711 | 5,964609 0,007460 | – 11,300129 4,222742 | – 6,513637 5,587913 | ||||
 |  |  |  |  |  |  | ||
| k=3 | – 0,867723 | 1,357711 – 1,178117 | 0,007460 5,964609 | 4,222742 – 11,300129 | 5,587913 – 6,513637 | |||
| Конеццикла | 5,971082 | – 7,635959 | – 1,664877 |
6. После этого выполняем обратный ход метода Гаусса. Находим неизвестные:




7. Выписываем полученное решение:

8. Так как в ходе решения вычисления выполнялись с округлением, то полученные значения неизвестных являются неточными. Поэтому для контроля расчета вычислим невязки, представляющие собой модули разностей между правыми и левыми частями уравнений системы:




Так как матрица системы хорошо обусловлена (во всех вариантах это условие выполняется) и невязки малы по модулю, то решение системы найдено достаточно точно.
9. Продолжаем выполнение работы в компьютерном классе. Запускаем программу Mathcad. Открываем файл Lab1.mcd. Вводим столбец свободных элементов и матрицу системы уравнений:

С помощью встроенной функции  (см. п. 6.4) пакета Mathcad для нахождения решения определенных систем линейных уравнений находим «точное решение»
(см. п. 6.4) пакета Mathcad для нахождения решения определенных систем линейных уравнений находим «точное решение»
 .
.
10. Выписываем полученное на компьютере решение

и вычисляем абсолютные погрешности, с какими найдены неизвестные в приближенном решении:

т. е. все погрешности меньше  и решение найдено достаточно точно.
и решение найдено достаточно точно.
11. Все расчеты оформляются в виде отчета по лабораторной работе.
Вопросы для самоконтроля
1. Что называется решением системы линейных алгебраических уравнений?
2. Какая система линейных алгебраических уравнений совместна, какая несовместна?
3. Какая совместная система линейных алгебраических уравнений определена, какая неопределена?
4. Что называется основной и расширенной матрицей системы линейных уравнений?
5. Что такое ранг матрицы A?
6. Сформулируйте теорему Кронекера-Капелли.
7. Когда система линейных алгебраических уравнений определена и когда неопределена?
8. Что такое элементарные преобразования строк матрицы?
9. Опишите структуру бланка расчета в методе Гаусса.
10. Как выполняется контроль текущих вычислений при реализации метода Гаусса?
11. Для чего предназначен контрольный столбец и как он формируется?
12. Опишите алгоритм прямого хода метода Гаусса и запишите расчетные формулы прямого хода.
13. Опишите алгоритм обратного хода метода Гаусса и запишите расчетные формулы обратного хода.
14. В чем состоит смысл выбора ведущей строки в методе Гаусса?
15. Что называется невязками уравнений системы?
