Метод скользящего среднего
Расчет прогноза и сглаживание временного ряда методом скользящего среднего производится по формуле
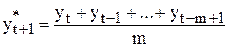 . . | (10.1) |
При этом предполагается, что все m значений 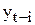 за m моментов времени вносят равный вклад в прогнозируемое значение
за m моментов времени вносят равный вклад в прогнозируемое значение 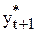 и учитываются с одинаковым весовым коэффициентом
и учитываются с одинаковым весовым коэффициентом 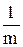 .
.
Метод экспоненциального сглаживания
В методе экспоненциального сглаживания весовые коэффициенты предыдущих наблюдаемых значений увеличиваются по мере приближения к последним (по времени) данным. Кроме того, в формировании прогнозируемого значения участвуют все n известных значений 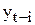 (
( 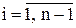 ) временного ряда
) временного ряда
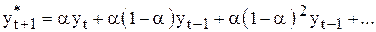 | (10.2) |
Для расчета прогноза и для сглаживания временного ряда методом экспоненциального сглаживания используют формулу (10.2) в виде
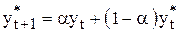 , , | (10.3) |
где 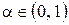 – константа сглаживания. Таким образом, значение
– константа сглаживания. Таким образом, значение 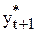 можно вычислить рекуррентно на основании значения
можно вычислить рекуррентно на основании значения 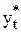 .
.
Методические рекомендации
Задача №10.01
Постройте и проанализируйте график временного ряда, представленного в табл.10.1 с точки зрения применимости методов скользящего среднего и экспоненциального сглаживания.
Таблица 10.1
Исходные данные задачи №10.01
| t | |||||||
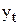 , тыс. шт. , тыс. шт. |
Сделайте прогноз для t=8 методом скользящей средней для m=4;методом экспоненциального сглаживания для a=0,6.
Решение
График исходного временного ряда представлен на рис.10.1.
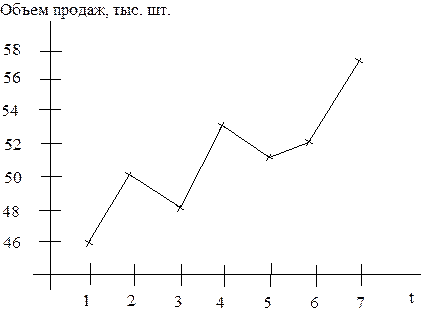
Рис.10.1.График временного ряда задачи №10.01
Из графика видно, что наблюдается явная тенденция к возрастанию значений временного ряда  , что приведет к неточности в прогнозах, выполненных методами скользящего среднего и экспоненциального сглаживания (это следует из допущений методов), к подавлению этой тенденции.
, что приведет к неточности в прогнозах, выполненных методами скользящего среднего и экспоненциального сглаживания (это следует из допущений методов), к подавлению этой тенденции.
Для прогнозирования методом скользящего среднего достаточно выполнить единственный расчет
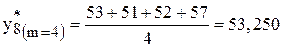 [тыс. шт.].
[тыс. шт.].
Для прогнозирования методом экспоненциального сглаживания необходимо провести расчеты для всех моментов времени, за исключением t=1:
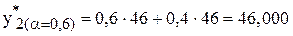 ;
;
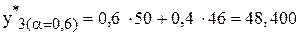 ;
;
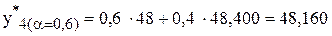 ;
; 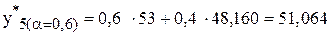 ;
;
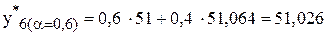 ;
; 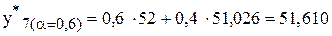 ;
;
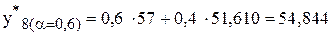 [тыс. шт.].
[тыс. шт.].
Не существует четкого правила для выбора числа членов скользящей средней m или параметра экспоненциального сглаживания 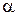 . Они определяются статистикой исследуемого процесса. Чем меньше m и чем больше a, тем сильнее реагирует прогноз на колебания временного ряда, и наоборот, чем больше m и чем меньше a, тем более инерционным является процесс прогнозирования. На практике величина n обычно принимается в пределах от 2 до 10, а
. Они определяются статистикой исследуемого процесса. Чем меньше m и чем больше a, тем сильнее реагирует прогноз на колебания временного ряда, и наоборот, чем больше m и чем меньше a, тем более инерционным является процесс прогнозирования. На практике величина n обычно принимается в пределах от 2 до 10, а 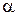 – в пределах от 0,01 до 0,30. При наличии достаточного числа элементов временного ряда значение m и a, приемлемое для прогноза, можно определить следующим образом:
– в пределах от 0,01 до 0,30. При наличии достаточного числа элементов временного ряда значение m и a, приемлемое для прогноза, можно определить следующим образом:
· задать несколько предварительных значений m ( 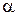 );
);
· сгладить временной ряд, используя каждое заданное значение m ( 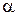 );
);
· вычислить среднюю ошибку прогнозирования как среднее абсолютное отклонение (mean absolut deviation – MAD)
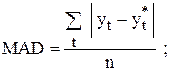 | (10.4) |
· выбрать значение m ( 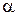 ), соответствующее минимальной ошибке.
), соответствующее минимальной ошибке.
Варианты задач для самостоятельного решения
Задача №10.1
В табл.10.2 приведены данные о спросе на некоторый товар за прошедшие два года.
Таблица 10.2
Объем спроса на товар
| Месяц t | Спрос 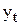 , тыс.шт. , тыс.шт. | Месяц t | Спрос 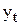 , тыс.шт. , тыс.шт. |
Постройте и проанализируйте график временного ряда с точки зрения применимости методов скользящего среднего и экспоненциального сглаживания. На основании анализа графика выберите наиболее приемлемое значение:
1) m из m=4 и m=8;
2) 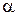 из
из 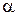 =0,05 и
=0,05 и 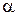 =0,3.
=0,3.
Проверьте свои предположения с помощью методики, описанной в п.10.2. Сделайте прогноз спроса на следующий месяц методом скользящего среднего и экспоненциального сглаживания.
Задача №10.2
В табл.10.3 содержатся данные за десятилетний период о количестве людей (Y), посетивших туристическую зону на воздушном транспорте.
Таблица 10.3
