Задачи для самостоятельного решения. Условие транспортной задачи задано распределительной таблицей

Задача № 5.3.

Условие транспортной задачи задано распределительной таблицей.

поставщики	потребители	запасы
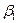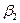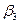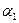потребности

Найти оптимальное распределение поставок и минимальные затраты на перевозку груза, выполнив первоначальное распределение методом наименьших затрат.

Задача № 5.4.

Однородный продукт, находящийся в трех пунктах производства, необходимо доставить в четыре пункта потребления. При этом матрица 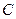транспортных затрат на перевозку единицы продукта из любого пункта отправления в любой пункт назначения, вектор объемов запасов продукта в пунктах производства и вектор объемов продукта, необходимых пунктам потребления, имеют вид:

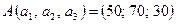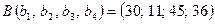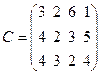Задача № 5.5.

Решить задачу №1.17.

Задача № 5.6.

Решить задачу №1.8.

Задача № 5.7.

Решить задачу №1.18.

Элементы теории игр

Ряд ситуаций в области экономики (особенно при наличии свободной конкуренции) принадлежит конфликтным ситуациям.

Конфликтная ситуация – ситуация, в которой две (или более) стороны преследуют различные цели, а результаты любого действия каждой из сторон зависят от действий партнера.

Для анализа подобных ситуаций был создан специальный математический аппарат – «Теория игр».

Целью теории игр является выработка рекомендаций по рациональному образу действий каждого из противников в ходе конфликтной ситуации.

Приведем основные понятия теории игр.

Игра - математическая модель конфликтной ситуации.

Степень удовлетворения своих интересов игроком может быть выражена числом, которое называется выигрышем.

Развитие игры во времени происходит с помощью последовательных этапов или «ходов». Ходом называется выбор одного из предусмотренных правилами игры вариантов. Ходы делятся на личные и случайные.

Личным ходом называется сознательный выбор одним из игроков одного из возможных в данной ситуации ходов. Любой из ходов в шахматы является личным ходом.

Случайным ходом называется выбор из ряда возможностей, осуществляемый не решением игрока, а каким-либо механизмом случайного выбора (бросание монеты, игральной кости, тасовка и сдача карт и т.д.).

Стратегия игрока – совокупность правил, определяющих выбор действий игрока при каждом личном ходе в зависимости от сложившейся ситуации.

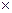В зависимости от числа возможных стратегий игры делятся на «конечные» и «бесконечные». Конечной называется игра, в которой у каждого игрока имеется только конечное число стратегий. Конечная игра, в которой игрок имеет m стратегий, а игрок – n стратегий, называется игрой m n.

Парная игра, в которой выигрыш одного из игроков равен проигрышу другого, называется игрой с нулевой суммой или антагонистической игрой.

Рассмотрим парную игру m 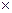n с нулевой суммой двух игроков и («мы» и «противник»). Обозначим наши стратегии 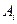(i=1,…m); стратегии противника обозначим 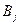(j=1,..,n).

Таблица, в которой заданы стратегии игроков и платежи, называется платежной матрицей. Если игра состоит только из личных ходов, то элементом платежной матрицы при применении игроками пары стратеги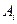й и 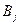будет платеж а_ij, равный выигрышу игрока . Если в игре присутствуют случайные ходы, то а_ij – это оценка ожидаемого выигрыша (математическое ожидание).

Платежная матрица m n имеет вид:

Таблица 6.1

		…		…
		…		…
…	…	…	…	…	…	…
		…		…
…	…	…	…	…	…	…
		…		…
		…		…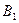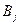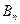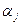
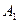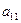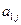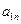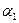
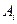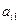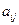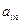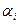
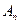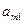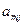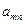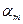
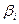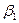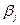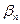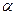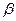