Решение систем линейных уравнений
Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х1, х2, …, хn:
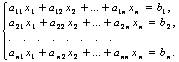
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричном виде: Ах = b,
где:
  |
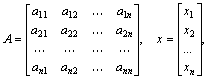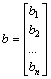Откуда, вектор решений находится из соотношения x=A(-1)*b
Например.
Решить систему уравнений: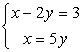 
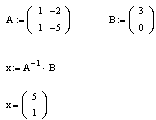
Задания
1. Ввести в документ название лабораторной работы, вариант задания и фамилию студента.
2. Ввести в документ текст: “Задание 1. Построение графиков”.
3. Построить графики заданных функций в декартовой системе координат заданным цветом с пересекающимися в начале координат осями и названием, не отображая выражения, задающие функции. Оба графика должны быть изображены сплошной линией, но разной толщины.
Вариант 1)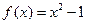 
, синий; 
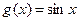,красный
Вариант 2)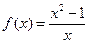 
, зеленый; 
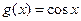, черный
Вариант 3)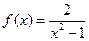 
, голубой; 
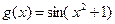, коричневый
Вариант 4)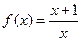 
,фиолетовый; 
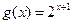, красный
Вариант 5)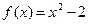 
, зеленый; 
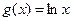, голубой
Вариант 6)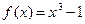 
, коричневый; 
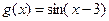, красный
Вариант 7)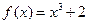 
, синий; 
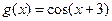, черный
Вариант 8)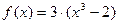 
, фиолетовый; 
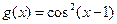, голубой
Вариант 9)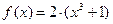 
, синий; 
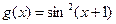, зеленый
Вариант 10) 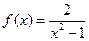, голубой; 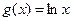, красный
Вариант 11) 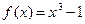, коричневый; 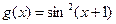, зеленый
Вариант 12) 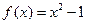, синий; 
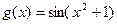, коричневый
Вариант 13)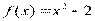 
, зеленый 
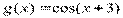, черный
Вариант 14)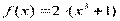 
, синий 
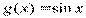,красный
Вариант 15)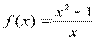 
, зеленый 
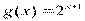, красный
Вариант 16)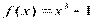 
, коричневый 
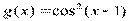, голубой
Вариант 17)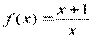 
,фиолетовый 
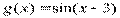, красный
Вариант 18)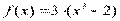 
, фиолетовый 
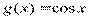, черный
Вариант 19)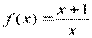 
,голубой 
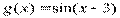, зелёный
Вариант 20) 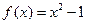, синий; 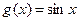,красный
Вариант 21) 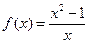, зеленый; 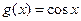, черный
Вариант 22) 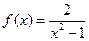, голубой; 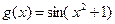, коричневый
Вариант 23) 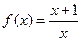,фиолетовый; 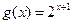, красный
Вариант 24) 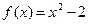, зеленый; 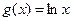, голубой
Вариант 25) 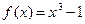, коричневый; 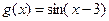, красный
Вариант 26) 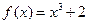, синий; 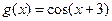, черный
Вариант 27) 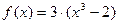, фиолетовый; 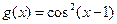, голубой
Вариант 28) 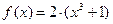, синий; 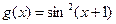, зеленый
Вариант 29) 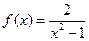, голубой; 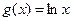, красный
Вариант 30) 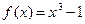, коричневый; 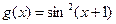, зеленый
Вариант 31) 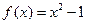, синий; 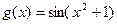, коричневый
Вариант 32)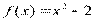 
, зеленый 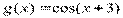, черный
Вариант 33)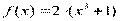 
, синий 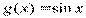,красный
Вариант 34)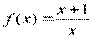 
,фиолетовый 
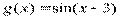, красный
Вариант 35)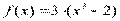 
, фиолетовый 
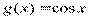, черный
Вариант 36)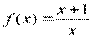 
,голубой 
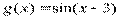, зелёный
Вариант 37)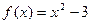 
, зеленый; 
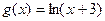, голубой
Вариант 38)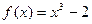 
, коричневый; 
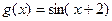, красный
Вариант 39)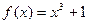 
, синий; 
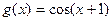, черный
4. Ввести в документ текст: “Задание 2. Работа с матрицами”.
5. Создать квадратные матрицы А, В размером (3,3), используя команду Insert - Matrix.
6. Найти определители матриц А и B, используя шаблон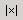 
, расположенный на панели “Матрицы”.
7. Для матрицы А найти транспонированную матрицу, используя шаблон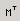 
.
8. Для матрицы В найти обратную матрицу, используя шаблон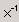 
.
9. Найти максимальный(минимальный) элемент матрицы А(В), используя команды min() и max()
10. Создать вектор C вторым способом (при помощи ранжированных переменных), количество элементов которого равно №. варианта
11. Применть к вектору С встроенные векторные функции, указанные в таблице.
12. Применить к матрице А встроенные матричные функции (2 функции) из приведенных в пункте “Функции для работы…..”
13. Ввести в документ текст: “Задание 3. Решение уравнений”
14. Решить уравнение, используя функцию root (задание взять из таблицы 1).
15. Решить уравнение, используя функцию polyroots (задание взять из таблицы 2).
16. Ввести в документ текст: “Задание 4. Решение систем уравнений”
17. Решить систему уравнений, сначала через блоки Given…Find, Given…Minerr а затем матричным способом (задание взять из таблицы 3).
18. Ввести в документ текст: “Задание 5. Программы для работы с массивами”
19. Разработать программу, выполняющую действия с массивом (задание 5).
| Таблица 1 | |||
| № варианта | Задание | № варианта | Задание |
 | | ||
 | | ||
 | | ||
 | | ||
 | | ||
 | | ||
 | | ||
 | | ||
 | | ||
 | | ||
 | | ||
 | | ||
| | | ||
| | | ||
| | | ||
| | | ||
| | | ||
| | | ||
| | | ||
| | |
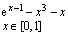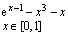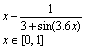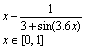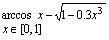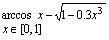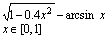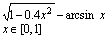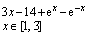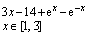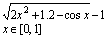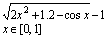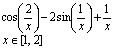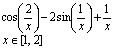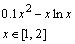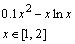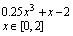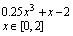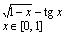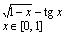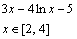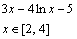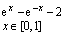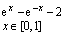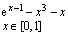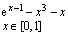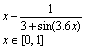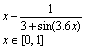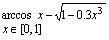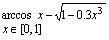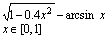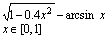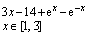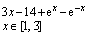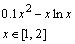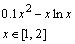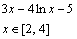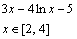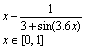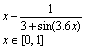| Таблица 2 | |||
| № варианта | Задание | № варианта | Задание |
| x4 - 2x3 + x2 - 12x + 20 | x4 - 4x3 - 2x2 - 20x + 25 | ||
| x4 + 6x3 + x2 - 4x - 60 | x4 + 5x3 + 7x2 + 7x - 20 | ||
| x4 - 14x2+x3 - 40x - 75 | x4 + 6x3 + x2 - 4x - 60 | ||
| x4 - x3 + x2 - 11x + 10 | x4 - 14x2+x3 - 40x - 75 | ||
| x4 - x3 - 29x2 - 71x -140 | x4 + 7x3 + 9x2 + 13x - 30 | ||
| x4 + 7x3 + 9x2 + 13x - 30 | x4 + x3 - 17x2 - 45x - 100 | ||
| x4 + 3x3 - 23x2 - 55x - 150 | x4 - 5x3 + x2 - 15x + 50 | ||
| x4 - 6x3 + 4x2 + 10x + 75 | x4 - 4x3 - 2x2 - 20x + 25 | ||
| x4 + x3 - 17x2 - 45x - 100 | x4 + 5x3 + 7x2 + 7x - 20 | ||
| x4 - 5x3 + x2 - 15x + 50 | x4 - 2x3 + x2 - 12x + 20 | ||
| x4 - 4x3 - 2x2 - 20x + 25 | x4 - 2x3 + x2 - 12x + 20 | ||
| x4 + 5x3 + 7x2 + 7x - 20 | x4 + 6x3 + x2 - 4x - 60 | ||
| x4 + 6x3 + x2 - 4x - 60 | x4 - 14x2+x3 - 40x - 75 | ||
| x4 - 14x2+x3 - 40x - 75 | x4 - x3 + x2 - 11x + 10 | ||
| x4 + 7x3 + 9x2 + 13x - 30 | x4 - x3 - 29x2 - 71x -140 | ||
| x4 + x3 - 17x2 - 45x - 100 | x4 + 7x3 + 9x2 + 13x - 30 | ||
| x4 - 5x3 + x2 - 15x + 50 | x4 + 3x3 - 23x2 - 55x - 150 | ||
| x4 - 4x3 - 2x2 - 20x + 25 | x4 - 6x3 + 4x2 + 10x + 75 | ||
| x4 + 5x3 + 7x2 + 7x - 20 | x4 + x3 - 17x2 - 45x - 100 | ||
| x4 - 2x3 + x2 - 12x + 20 | x4 - 5x3 + x2 - 15x + 50 |
| Таблица 3 | |||
| № варианта | Задание | № варианта | Задание |
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
 |  | ||
| | | ||
 | | ||
 | | ||
 | | ||
 | | ||
| | | ||
 | | ||
 | | ||
 | | ||
 | | ||
 | | ||
 | | ||
 | | ||
 | |
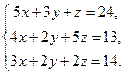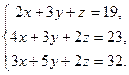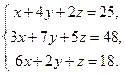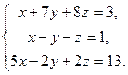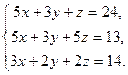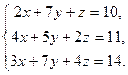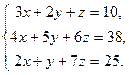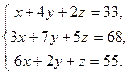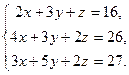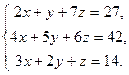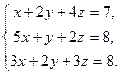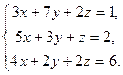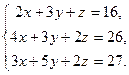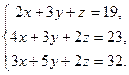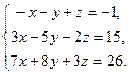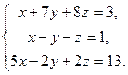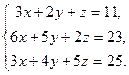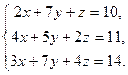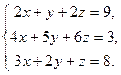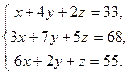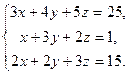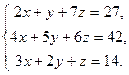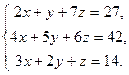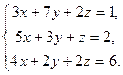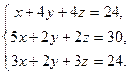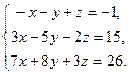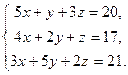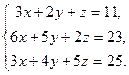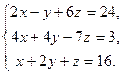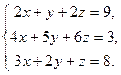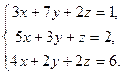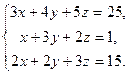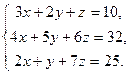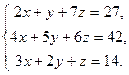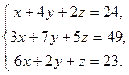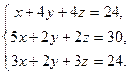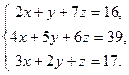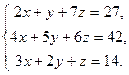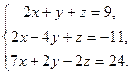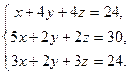Задание 5.
1) Подсчитать количество положительных и количество отрицательных элементов массива X(20).
2) Вычислить значения функции z=sqrt((xi+ai)/2), если xi и ai - элементы массивов, состоящих из десяти элементов каждый.
3) Найти сумму положительных и сумму отрицательных элементов массива X(11).
4) Задан массив X, состоящий из пяти элементов. Вычислить значения функции y=0.5*ln(x) при значениях аргумента, заданных в массиве X, и поместить их в массив Y.
5) Даны два массива X(10) и Y(8). Сформировать массив Z(18) из положительных элементов массивов X и Y. Если положительных элементов меньше 18, то оставшимся элементам массива Z присвоить значение +1.
6) В матрице A(6,6) найти произведение положительных элементов главной диагонали и сумму всех элементов побочной диагонали.
7) Задана матрица M(3,4). Определить, сколько чисел больше -2, но меньше 2 находится в третьей строке.
8) Дан массив A(20). Определить, сколько его элементов с номерами 1, 2, 4, 8, 16 имеют значение меньше, чем 0.25.
9) Дан массив целых чисел C(17). Имеются ли в этом массиве два идущих подряд нулевых элемента.
10) Дан массив X(14). Заменить все элементы массива, значения которых меньше 2, нулями.
11) Задан массив Y(24). Определить количество элементов, которые при делении на 7 дают остаток 1, 2 или 5.
12) Дан массив Q(23). Получить сумму тех элементов массива, которые нечетны и отрицательны.
13) В матрице B(7,3) найти сумму всех положительных элементов, количество отрицательных элементов, а если Bij=0, то вместо него записать +1.
14) В матрице A(5,4) подсчитать количество элементов, удовлетворяющих условию K1 <= Aij <= K2 или Aij > i+j, где K1 и K2 - произвольные числа.
15) Дана матрица B(4,4). Среди элементов главной диагонали найти наименьший, вывести его, и, если он меньше некоторого числа K, то ко всем элементам строки, в которой расположен наименьший элемент, прибавить 1.
16) В матрице C(4,4) подсчитать количество элементов, удовлетворяющих условию K2<=|Cij|<=K2 (K1 и K2 - произвольные числа), и подсчитать их сумму
17) В матрице Z(6,6) найти максимальный элемент, расположенный на главной диагонали, и произведение всех отрицательных элементов матрицы
18) Среди элементов, расположенных ниже главной диагонали матрицы A(6,6), найти те элементы, которые удовлетворяют условию K2 <= Aij <= K1 (K1, K2 - произвольные числа), и сформировать из них одномерный массив.
19) Среди элементов, расположенных ниже главной диагонали матрицы B(6,6), найти элементы, удовлетворяющие условию Bij<=K и Bij>i+j, и сформировать из них одномерный массив X.
20) Дана матрица B(4,4). Среди элементов главной диагонали найти наименьший элемент, вывести его на печать, и, если он меньше некоторого числа K, ко всем элементам строки, в которой он расположен, прибавить +1.
21) В матрице C(6,6) найти сумму S1 и S2 элементов, расположенных выше и ниже главной диагонали.
22) В матрице H(5,5) найти минимальный элемент среди элементов, расположенных ниже побочной диагонали, и количество элементов матрицы, значение которых не больше некоторого числа K.
23) Из массивов X(15) и Y(10) построить матрицу A(5,5) таким образом, чтобы элементы массива X были расположены на главной диагонали и выше ее.
24) В матрице D(6,6) найти произведение элементов, расположенных на главной диагонали и выше ее, причем Dij<>0. Подсчитать количество элементов Dij=0.
25) В матрице C(6,6) найти произведение P1 и P2 не равных нулю элементов, расположенных выше и ниже главной диагонали
26) Найти сумму положительных и сумму отрицательных элементов массива X(11).
27) Задан массив X, состоящий из пяти элементов. Вычислить значения функции y=0.5*ln(x) при значениях аргумента, заданных в массиве X, и поместить их в массив Y.
28) Даны два массива X(10) и Y(8). Сформировать массив Z(18) из положительных элементов массивов X и Y. Если положительных элементов меньше 18, то оставшимся элементам массива Z присвоить значение +1.
29) В матрице A(6,6) найти произведение положительных элементов главной диагонали и сумму всех элементов побочной диагонали.
30) Задана матрица M(3,4). Определить, сколько чисел больше -2, но меньше 2 находится в третьей строке.
31) Дан массив A(20). Определить, сколько его элементов с номерами 1, 2, 4, 8, 16 имеют значение меньше, чем 0.25.
32) Дан массив целых чисел C(17). Имеются ли в этом массиве два идущих подряд нулевых элемента.
33) Дан массив X(14). Заменить все элементы массива, значения которых меньше 2, нулями.
34) Задан массив Y(24). Определить количество элементов, которые при делении на 7 дают остаток 1, 2 или 5.
35) Дан массив Q(23). Получить сумму тех элементов массива, которые нечетны и отрицательны.
36) В матрице B(7,3) найти сумму всех положительных элементов, количество отрицательных элементов, а если Bij=0, то вместо него записать +1.
37) В матрице A(5,4) подсчитать количество элементов, удовлетворяющих условию K1 <= Aij <= K2 или Aij > i+j, где K1 и K2 - произвольные числа.
38) Дана матрица B(4,4). Среди элементов главной диагонали найти наименьший, вывести его, и, если он меньше некоторого числа K, то ко всем элементам строки, в которой расположен наименьший элемент, прибавить 1.
39) В матрице C(4,4) подсчитать количество элементов, удовлетворяющих условию K2<=|Cij|<=K2 (K1 и K2 - произвольные числа), и подсчитать их сумму
40) В матрице Z(6,6) найти максимальный элемент, расположенный на главной диагонали, и произведение всех отрицательных элементов матрицы