Оценка существенности связи
После того, как значения коэффициентов получены, следует проверить их значимость. Поскольку исходные данные, по которым устанавливается взаимосвязь признаков, являются определенной выборкой из некоей генеральной совокупности объектов, исчисленные по этим данным парные коэффициенты корреляции будут выборочными. Таким образом, они лишь оценивают связь исходя из той информации, которую несут отобранные единицы наблюдения. Если исходные данные «хорошо» отражают структуру и закономерности генеральной совокупности, то и исчисленный по ним коэффициент корреляции будет показывать реальную связь, присущую в действительности всей исследуемой совокупности объектов. Если данные не «копируют» взаимосвязи совокупности в целом, то и рассчитанный коэффициент корреляции сформирует ложное представление о зависимости. В идеале, чтобы установить этот факт, требуется исчислить коэффициент корреляции на основе данных всей совокупности и сравнить его с исчисленным по отобранным наблюдениям. Однако на практике, как правило, этого сделать нельзя, так как зачастую неизвестна вся генеральная совокупность или же она слишком велика. Поэтому о том, насколько реально коэффициент представляет действительность, можно судить лишь приблизительно. На основе логики легко прийти к выводу, что, очевидно, с увеличением числа наблюдений (при n → N) доверие к исчисленному коэффициенту будет увеличиваться.
Значимость парных коэффициентов корреляции проверяется одним из двух способов: с помощью таблицы Фишера - Йейтса или по t-критерию Стьюдента. Рассмотрим способ проверки с помощью таблицы Фишера - Йейтса как наиболее простой.
В начале проверки задается уровень значимости (чаще всего обозначаемый буквой греческого алфавита «альфа» ¾ a), который показывает вероятность принятия ошибочного решения. Возможность совершить ошибку вытекает из того факта, что для определения взаимосвязи используются данные не всей совокупности, а лишь ее части. Обычно aпринимает следующие значения: 0,05; 0,02; 0,01; 0,001. Например, если a = 0,05, то это означает, что в среднем в пяти случаях из ста принятое решение о значимости (или незначимости) парных коэффициентов корреляции будет ошибочным; при a = 0,001 ¾ в одном случае из тысячи и т. д.
Вторым параметром при проверке значимости является число степеней свободы n, которое в данном случае вычисляется как n= n - 2. По таблице Фишера - Йейтса находится критическое значение коэффициента корреляции rкр.(a = 0,05, n = n - 2). Коэффициенты, значения которых по модулю больше найденного критического значения, считаются значимыми.
Пример 2. Предположим, что в первом случае имеется 12 наблюдений, и по ним вычислили парный коэффициент корреляции, который оказался равным 0,530, во втором ¾ 92 наблюдения, и рассчитанный парный коэффициент корреляции составил 0,36. Но если мы проверим их значимость, в первом случае коэффициент окажется незначимым, а во втором ¾ значимым, невзирая на то, что он по величине гораздо меньше. Оказывается, в первом случае слишком мало наблюдений, что повышает требования, и критическая величина парного коэффициента корреляции при уровне значимости a = 0,05 составляет 0,576 (n = 12 - 2), а во втором ¾ наблюдений значительно больше и достаточно превысить критическое значение 0,205 (n = 92 - 2), чтобы коэффициент корреляции при том же уровне a оказался значимым. Таким образом, чем меньше наблюдений, тем всегда будет выше критическое значение коэффициента.
Проверка значимости по существу решает вопрос, случайны или нет полученные результаты расчетов.
Определение множественного коэффициента корреляции
Следующий этап корреляционного анализа связан с расчетом множественного (совокупного) коэффициента корреляции.
Множественный коэффициент корреляции характеризует тесноту линейной связи между одной переменной и совокупностью других переменных, рассматриваемых в корреляционном анализе.
Если изучается связь между результативным признаком y и лишь двумя факторными признаками х1и х2, то для вычисления множественного коэффициента корреляции можно использовать следующую формулу, компонентами которой являются парные коэффициенты корреляции:
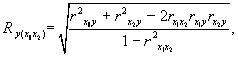
где r ¾ парные коэффициенты корреляции.
Регрессионный анализ
