Методические рекомендации. Расчет электрической цепи постоянного тока состоит в определении неизвестных токов в
Расчет электрической цепи постоянного тока состоит в определении неизвестных токов в ветвях.
Решение может быть проведено одним из трех способов:
1) по законам Кирхгофа;
2) методом контурных токов;
3) методом узловых потенциалов.
Таблица 2- Данные к задаче 1
| Номер схемы | Схема к задаче 1 |
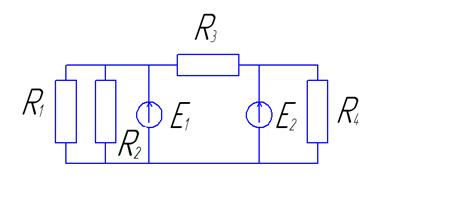 | |
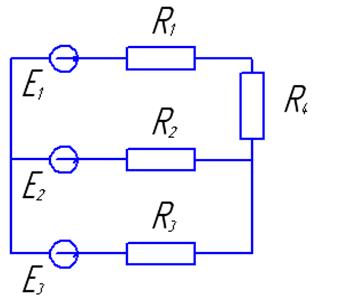 | |
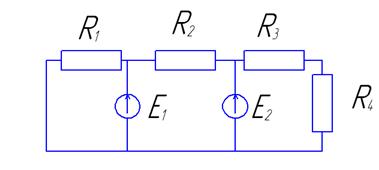 | |
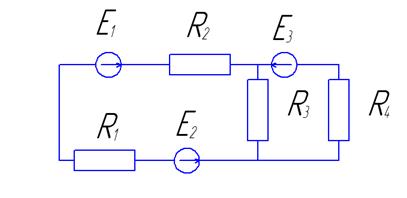 |
Последовательность решения задачи
1. Составить систему линейных уравнений относительно неизвестных токов.
2. Разработать алгоритм решения, предусмотрев в нем ввод исходных данных, вызов стандартной или собственной подпрограммы численного
решения системы уравнений и вывод полученных результатов.
3. Применить программу, реализующую алгоритм на языке программирования высокого уровня, например на Бейсике. При этом следует обратить внимание на:
- вызов подпрограммы численного решения и передачу ей параметров;
- наглядность и удобство ввода и вывода данных.
Текст стандартной подпрограммы следует привести в решении и прокомментировать.
Задача 2.
Разработать математическую модель, алгоритм и использовать программу для расчета угловой скорости механизма по заданному моменту на валу М и моменту нагрузки Мнагр.
Методические рекомендации
До начала рассматриваемого процесса механизм неподвижен. Рассматриваемый переходный процесс описывается уравнением движения:
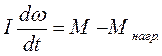
Необходимо подставить в уравнение выражения для М и Мнагр,, соответствующие варианту, и выразить из уравнения производную угловой скорости.
Дальнейшее решение повторяет действия 2 и 3 первой задачи, с той разницей, что вместо подпрограммы решения системы линейных уравнений следует использовать подпрограмму численного решения дифференциального уравнения.
Таблица3
Данные к задаче 2
| Вариант | M(t) | Мнагр.(t) |
| M = М0e-t/T | Мнагр.= βω | |
| M = М0e-t/T | Мнагр.= βω2 | |
| M = М0e-t/T | Мнагр.= const | |
| M = М0e-t/T | Мнагр.= Мср. + ΔМ sin ωм t | |
| M = М0e-t/T | Мнагр.= Мср. + ΔМ cos ωм t | |
| M = const | Мнагр.= βω | |
| M = const | Мнагр.= βω2 | |
| M = const | Мнагр.= const | |
| M = const | Мнагр.= Мср. + ΔМ sin ωм t | |
| M = const | Мнагр.= Мср. + ΔМ cos ωм t |
Задача 3.1- для специальностей -“Механизация сельского хозяйства”, “Технология обслуживания и ремонта машин в АПК”.
Задача 3.2 - для специальностей -“Механизация переработки сельскохозяйственной продукции”, “Технология продуктов общественного питания”.
Задача 3.3предусмотренадля всех специальностей.
Задача об использовании ресурсов
Общая постановка
Для изготовления nвидов продукции P1,…, Pn предприятие использует m видов ресурсов S1, …, Sm (сырьё, топливо, материалы и т. д.).
Запасы ресурсов каждого вида ограничены и равны b1, …, bm.
На изготовление единицы продукции j-го вида (j=1, …,n) расходуется aij единиц i-го ресурса (i = 1,…, n).
При реализации единицы j-й продукции предприятие получает Cj единиц прибыли.
Необходимо составить такой план выпуска продукции, чтобы при её реализации получить максимальную прибыль.
Пример: (ориентировочный его не переписывать! При выполнении вариантного задания студент формулирует задачу самостоятельно исходя из требований профессиональной деятельности.)
АО “КВАНТ” производит 3 вида продукции: спальный гарнитур “КОМФОРТ”, кухонный гарнитур “УЮТ”, мягкую мебель “ОТДЫХ”. При этом использует 4 вида ресурсов: ламинат - (облицованная пластиком ДСП), конферматы - (шурупы-саморезы), гобелен - (мебельная ткань), поролон.
Запасы ресурсов составляют: ламината - 25 м2, конферматов - 14 комплектов, гобелена – 19 рулонов, поролона – 24 м2.
На изготовление одного спального гарнитура расходуется: ламината – 2 м2, конферматов –1 комплект, гобелена –1 рулон, поролона–3 м2. Для кухонного гарнитура и мягкой мебели данные в таблице 4.
При реализации гарнитура “КОМФОРТ” АО “КВАНТ” получает прибыль 600 рублей, гарнитура “УЮТ”-550 рублей, мебели “ОТДЫХ” -750 РУБЛЕЙ.
Требуется составить такой план выпуска продукции, чтобы при её реализации АО “ КВАНТ” получило максимальную прибыль.
Таблица 4-Варианты задач об использовании ресурсов
| Ва-риант | Виды ресур-сов | Расход ресурсов на единицу продукции | Запа-сы ре-сурсов | Доход от реализации единицы продукции | ||||
| P 1 | P2 | P3 | Cp1 | Cp2 | Cp3 | |||
| S1 | ||||||||
| S2 | ||||||||
| S3 | ||||||||
| S4 | ||||||||
| S1 | - | |||||||
| S2 | - | |||||||
| S3 | - | - | ||||||
| S4 | - |
Продолжение таблицы 4
| S1 | - | |||||||
| S2 | - | - | ||||||
| S3 | - | |||||||
| S1 | - | |||||||
| S2 | - | |||||||
| S3 | - | - | ||||||
| S4 | - | |||||||
| S1 | ||||||||
| S2 | ||||||||
| S3 | ||||||||
| S4 |
3.2. Задача о смесях
К этому типу относятся разнообразные задачи на составление рациона питания, смесей из нескольких компонентов (продуктов, материалов и т.п.) для получения конечного продукта с заданными свойствами. В математическом плане к этому виду относятся также некоторые задачи планирования производства. Рассмотрим формулировку задачи о смеси.
Имеется n продуктов P 1,…,P n, содержащих m питательных веществ S1,…, Sm. Пусть a ij , i = 1,…,n; j = 1,…,m , - количество единиц j-го питательного вещества в единице j-го продукта; b j – суточная потребность (минимальная норма) организма в j-м питательном веществе; C 1 – стоимость единицы i-го продукта.
Требуется выбрать такой суточный рацион питания (т.е. назначить количество продуктов P 1,… P n, входящих в него), чтобы условия по питательным веществам были выполнены, а стоимость рациона была минимальной.
Варианты ориентировочных данных задачи приведены в таблице 5.
Таблица 5. –Данные к задаче о смесях
| Вариант | Виды пита-тель-ных ве-ществ | Количество единиц питательных веществ в единице продукции | Минималь-ная норма питатель-ных ве-ществ | Стоимость единицы продукта | ||||||
| P1 | P2 | P3 | P4 | CP1 | CP2 | CP3 | CP4 | |||
| S1 | - | - | ||||||||
| S2 | - | - | - | - | ||||||
| S3 | - | - | ||||||||
| S1 | 1.2 | 1.4 | 0.8 | - | 1.6 | |||||
| S2 | - | - | ||||||||
| S3 | - |
| S1 | 26.5 | 7.8 | ||||||||
| S2 | 45.7 | 14.4 | 12.8 | |||||||
| S3 | 72.5 | |||||||||
| S1 | - | - | ||||||||
| S2 | - | - | ||||||||
| S3 | - | - | - | - | ||||||
| S4 | - | - | ||||||||
| S5 | - | - | ||||||||
| S1 | 0.18 | 0.24 | 1.2 | - | ||||||
| S2 | - | 1.1 | 7.5 | - | ||||||
| S3 | 1.5 | - |
3.3. Задача о загрузке оборудования
Рассмотрим две постановки этой задачи.
1. Предприятие выпускает n видов изделий P 1,…,Pn, каждое из которых проходит последовательную обработку на станках типов T 1,…, T m . Запас мощности станков, т.е. рабочее время станка, составляет соответственно b 1,…, bm единиц времени. Изделие P i обрабатывается первым станком (типа Т1) ai 1 единицвремени, вторым станком – a i 2 единиц времени и т.д. При реализации одно изделие P i приносит предприятию C i единиц прибыли (i = 1,…, n). Составить такой план загрузки станков, при котором предприятие получит максимальную прибыль. Конкретные числовые данные приведены в таблице 6.
2. Предприятию необходимо выпустить n видов изделий P 1,…, Pn в количествах соответственно N1,…, Nn единиц. Для этой цели используются т типов станков T1,…, Tm, каждый из которых может обрабатывать все изделия Pi, i = 1,…, n. Производительность каждого станка (количество изделий, обрабатываемых в единицу времени) имеет величину a i j , i = 1,…,n; j = 1,…, m. Запас мощности станков (рабочее время станка) составляет соответственно b1,…, bm единиц времени . составить такой план загрузки станков, при котором себестоимость выпуска продукции будет минимальной. Ориентрировочные числовые данные приведены в таблице 7.
Таблица 6- Первый вариант задачи о загрузке оборудования
| Вариант | Типы стан-ков | Продолжительность обработки изделия на станке | Доход от реализации изделия | Запас мощ-ности станков | ||||
| P1 | P2 | P3 | Cp1 | Cp2 | Cp3 | |||
| T1 | ||||||||
| T2 | ||||||||
| T3 |
| T1 | ||||||||
| T2 | ||||||||
| T3 | ||||||||
| T4 | ||||||||
| T1 | ||||||||
| T2 | ||||||||
| T3 | ||||||||
| T1 | ||||||||
| T2 | ||||||||
| T3 | ||||||||
| T1 | ||||||||
| T2 | ||||||||
| T3 |
Таблица 7- Второй вариант задачи о загрузке оборудования
| Ва-риант | Типы стан-ков | Производительность станков | Себестоимость продукции | План выпуска продукции | Запас мощ-ности стан-ков | |||||||||
| P1 | P2 | P3 | P4 | Cp1 | Cp2 | Cp3 | Cp4 | Np1 | Np2 | Np3 | Np4 | |||
| T1 | ||||||||||||||
| T2 | ||||||||||||||
| T3 | ||||||||||||||
| T1 | ||||||||||||||
| T2 | ||||||||||||||
| T1 | 0.5 | 1.2 | ||||||||||||
| T2 | 0.8 | 1.2 | 0.9 | 0.8 | 4.5 | 1.5 | ||||||||
| T3 | 0.5 | 0.6 | 0.9 | |||||||||||
| T1 | ||||||||||||||
| T2 | ||||||||||||||
| T1 | 1.5 | |||||||||||||
| T2 | 1.7 | 3.3 | ||||||||||||
| T3 | 2.5 |
