Правила дифференцирования

1) Производная константы равна нулю, т.е 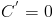, где C – константа.

2) Производная суммы (разности) равна сумме (разности) производных, т.е . .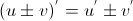

3) Производная произведения находится по правилу: .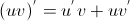

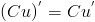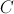4) , где - константа.

5) Производная дроби находится по правилу: .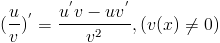

6) Если функция 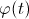имеет производную в точке 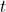, а функция 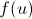имеет производную в точке 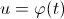, то сложная функция 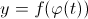имеет производную в точке 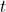, причем 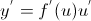(правило дифференцирования сложной функции).

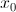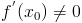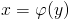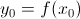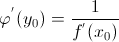7) Пусть функция y = f(x) имеет производную в точке , причем . Если существует обратная функция , то она имеет производную в точке и (производная обратной функции).

26) Теорема. Ролля. Если функция g(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка и на концах обращается в нуль g(a)=g(b)=0, то существует по крайней мере одна точка a < c < b в которой производная g¢ обращается в нуль g¢(c)=0.

Доказательство.Так как функция непрерывна на [a,b], то она имеет на этом отрезке наибольшее (M) и наименьшее значение m. Пусть g(c) - наибольшее значение.

Отсюда

g(c+Dx) - g(c) Dx £ 0, Dx > 0

g(c+Dx) - g(c) Dx ³ 0, Dx < 0

Переходим к пределу и получаем одновременно g¢(с) ³ 0 и g¢(с) £ 0, следовательно, g¢(с)=0.

Пример функции, для которой не выполняется условие теоремы, поэтому производная внутри отрезка в 0 не обращается

y=1-(x2)1/3

Теорема. Лагранжа. Если функция g(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка, то существует по крайней мере одна точка a < c < b в которой выполняется равенство

g(b)-g(a)=g¢(c)(b-a)

Доказательство.Применим теорему Ролля к функции

g(x)-g(a)-(x-a)Q,

где

Q=(g(b)-g(a))/(b-a)

Теорема. Коши. Если функции g(x) и h(x) непрерывны на отрезке [a,b], дифференцируемы во всех внутренних точках этого отрезка, причем h¢(x) ¹ 0 внутри отрезка [a,b], то существует точка a < c < b в которой выполняется равенство

g(b)-g(a) h(b)-h(a) = g¢(c) h¢(c)

Доказательство.Применим теорему Ролля к функции

g(x)-g(a)-(h(x)-h(a))Q,

где

Q=(g(b)-g(a))/(h(b)-h(a))

Теорема. Лопиталя. Пусть функции g(x) и h(x) на некотором отрезке [a,b] удовлетворяют условиям теоремы Kоши и обращаются в 0 в точке x=a, т.е. g(a)=h(a)=0, тогда если существует предел отношения g¢(x)/h¢(x) при x® a, то существует и

lim x® a g(x)/h(x)

27) Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть 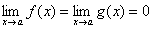или 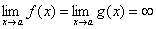. Тогда, если существует предел отношения производных этих функций 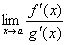, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

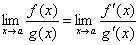(1)

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

28) Формула Тейлора и Маклорена .

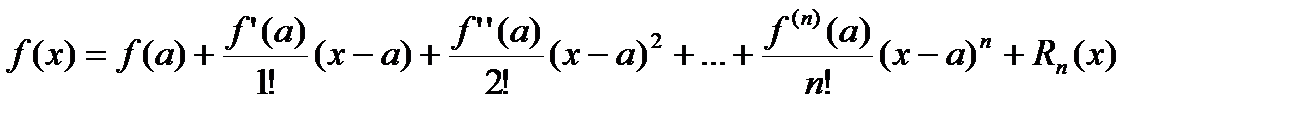
Формула Тейлора

f(x)= P(x) -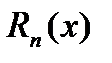

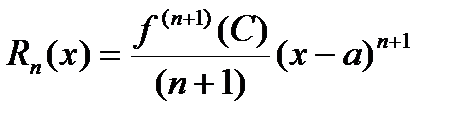
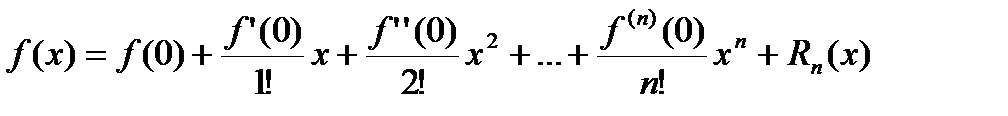
Формула Маклорена

2; Разложение Многочлена на Множители:

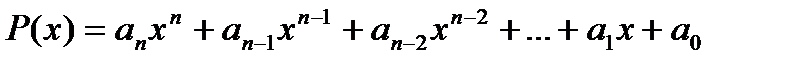
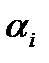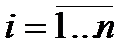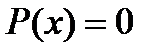
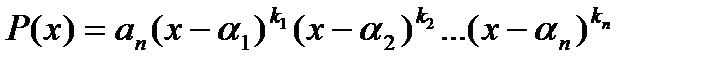,( ) корени

при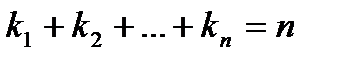

29)

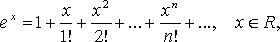
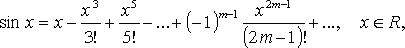
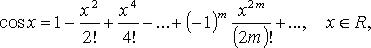
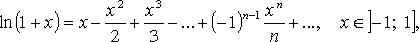
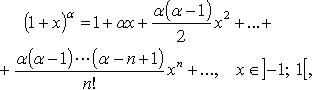
30) Теорема.(Необходимое условие экстремума).Если функция y =f(x) в точке х₀ имеет экстремум, то производная f^/( x ₀ ) равна нулю.

О.Точка, в которой производная равна нулю, называется стационарной.

Стационарная точка необязательно является точкой экстремума функции.

О. Точка в которой производная функции равна 0 или не существует, называется критической точкой.