Комплексные числа (26)
Натуральные числа N: 0,1,2,3,… Целые числа: 0,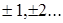 
Рациональные числа: 1/2,1/3, 3/5 Иррациональные числа: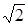 
и т. д.
Все это действительные числа. Обобщением действительных чисел являются комплексные числа z=x+iy где x-действительная часть комплексного числа ReZ,
y- мнимая часть комплексного числа ImZ, i- мнимая единица i2=-1
Z=x+iy=ReZ+iImZ (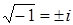 
), Z=x+iy называется алгебраической формой записи числа. Если ImZ=0, то Z=x – действительное число. Если ReZ=0, то Z=iy – число мнимоекомплексные число. Если ReZ= ImZ=0, то Z=0
Два комплексных числа Z1=x1+iy1, и Z2=x2+iy2 называются равными если ReZ1=ReZ2 (x1=x2) и ImZ1= ImZ2 (y1=y2). Комплексное число Z=x+iy и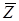 
называются комплексно сопряженными.
Геометрический смысл комплексных чисел:
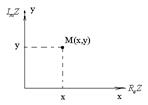Рассмотрим Z=x+iy. Каждому Z ставится в соответствии точка M(x,y) на комплексной плоскости 
Z и наоборот.
Ось OX (абсцисс) называется действительной осью, а ось OY (ординат) называется мнимой осью.
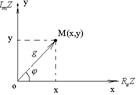Рассмотрим вектор: Любому вектору 
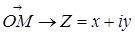и преобразуем. Возьмем полярную систему координат 
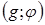точка M(x,y)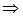 
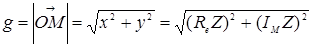
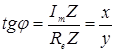
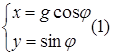, g – называется модулем комплексного числа, а 
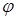- аргументом числа Z ( 
). 
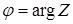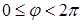и определены неоднозначно а с точностью до числа кратного 
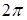. Используя формулу (1) получим тригонометрическую форму записи комплексного числа 
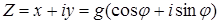. Используя формулу Эллера получим: 
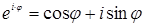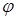, - действительные числа. 
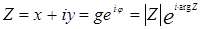Рассмотрим частные случаи:
Если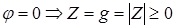 
- действительные числа. Если 
, 
, 
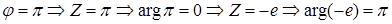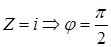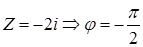. В общем случаи: Модуль комплексного числа 
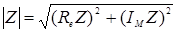, argZ находится из уравнения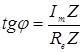 
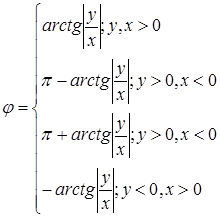Пример: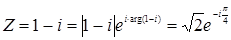 
ReZ=1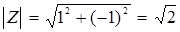 
ImZ=-1 
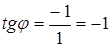
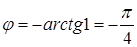
Замечание: Комплексно сопряженные числа Z=x+iy и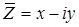 
геометрически изображаются двумя точками на комплексной плоскости зеркально симметричны относительно действительной оси (ReZ). В показательной форме 
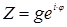, то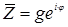 
.
Действия над комплексными числами (27).
1. Сложение: Суммой двух комплексных чисел Z1=x1+iy1 и Z2=x2+iy2 называется Z=Z1+Z2=(x1+x2)+i(y1+y2). 2. Вычитание: Разностью двух комплексных чисел Z1=x1+iy1 и Z2=x2+iy2 называется Z которое будучи сложенным с Z2 дает Z1 Z=Z1+Z2=>Z1=Z2+Z=(x1-_x2)+i(y1-y2), при сложении и вычитании комплексных чисел они должны быть представлены в алгебраической форме.
3. Умножение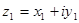 
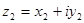
Пр-ем комплексных чисел z1 b z2 называется такое комплексное число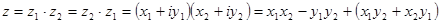 
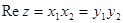
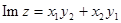
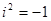
Пр-р: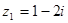 
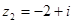
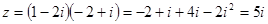
Если к.ч. 
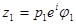
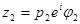, то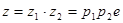 
Деление.
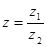такое к.ч. 
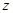, что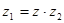 
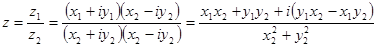
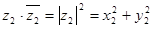
определения деления сводится к определении умножения.
Пример: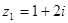 
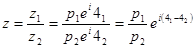
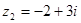
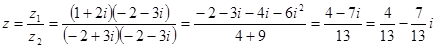
Возведение к.ч. в целую степень.
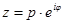
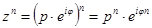
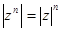
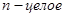
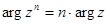
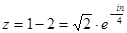
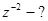
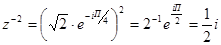
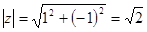
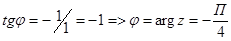
(IV)
Возведение к.ч. в дробную степень извлечения корня.
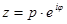
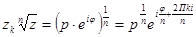
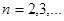
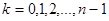
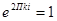
Имеются n различных к.4. Zк, кат. имеют 1 и тот же модуль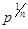 
, а их аргументы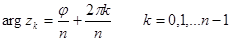 
Все эти к.ч. лежат на окружности радиусом 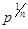в вершинах правильного n-угольника, вписанного в эту окружность(n>=3). При n=2- на концах диаметра этой окружности.