Таблицы истинности. Тождественно истинные и тождественно ложные высказывания
Отрицанием высказывания х называется новое высказывание, которое истинно, если высказывание ложное и наоборот. Таблица истинности операции отрицания имеет вид:
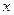 | 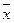 |
Дизъюнкцией двух высказываний x и y(логическое «или»)называется новое высказывание, которое будет истинным тогда когда, когда хотя бы одно из высказываний будет истинным.
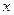 | 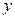 | 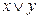 |
Конъюнкцией двух высказываний x и y(логическое «и»)называется новое высказывание, которое будет истинным тогда когда, когда оба высказывания истины. Обозначение операции конъюнкция - &( 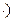
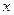 | 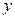 | 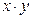 |
Импликацией двух высказываний x и y(«если – то») называется новое высказывание, которое ложно тогда, когда х(предпосылка)- истинно, а у(следствие)- ложно.
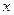 | 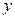 | 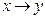 |
Эквивалентностью двух высказываний x и y(«тогда и только тогда») называется новое высказывание, которое будет истинно , если высказывания х и у будут одновременно истинны или ложны.
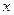 | 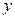 | 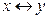 |
Неодназночностью (суммой по модулю два) двух высказываний x и y(«тогда и только тогда») называется новое высказывание, которое будет истинно тогда когда одно из высказываний х или у истинно, а другое ложно.
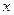 | 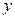 | 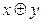 |
Штрих Шеффера (логическое «и - не») высказываний x и y - это новое высказывание, которое будет ложно тогда и только тогда когда оба высказывания истинны.
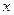 | 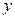 | 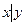 |
Стрелка Пирса (логическое «или - не») высказываний x и y - это новое высказывание, которое будет истинно тогда и только тогда когда оба высказывания ложны.
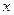 | 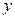 | 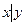 |
Для операций справедливы следующие приоритеты: ù, &, Ú, ®, «.
Тождественные высказывания. Среди высказываний особое место занимают те, в таблице истинности которых либо одни единицы, либо только нули. Это означает, что высказывание либо всегда истинно, либо ложно, независимо от истинности входящих в него высказываний. Например, высказывание 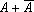 всегда истинно, а высказывание
всегда истинно, а высказывание 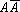 всегда ложно. Доказать это можно составив таблицу истинности этих высказываний.
всегда ложно. Доказать это можно составив таблицу истинности этих высказываний.
Сложные высказывания, истинные при любых значениях входящих в них других высказываний, называются тождественно истинными, а высказывания, ложные при любых значениях входящих в них других высказываний, называются тождественно ложными.
Тождественно истинные или тождественно ложные высказывания, если они встречаются в формулах, заменяются в них, соответственно единицей или нулем:
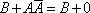 ,
, 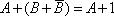 .
.
Среди высказываний встречаются такие, таблицы истинности которых совпадают. Эти высказывания называются эквивалентными. Эквивалентными являются, например, высказывания 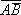 и
и 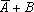 (то есть
(то есть 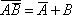 ).
).
Билет№17
