Периодичность функции

Функция 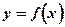называется ПЕРИОДИЧЕСКОЙ, если для нее существует такое число Т ¹ 0, называемое периодом функции, что при любых x из области определения функции числа x–T и x+T также принадлежат этой области и выполняется равенство

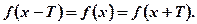
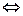
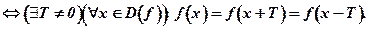периодическая (8. 9)

Отрицанием факта периодичности функции 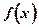является утверждение:

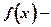непериодическая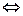

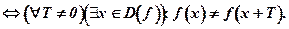(8. 10)

То есть функция является непериодической, если для любых отличных от нуля Т найдется (хотя бы одно) значение аргумента х, что .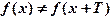

Если число Т является периодом функции, то число nТ при любом 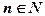–тоже период функции. Наименьший положительный период функции, когда он существует, называют основным периодом функции или просто периодом.

Покажем, например, что функция

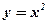
не является периодической.

Действительно, чтобы по любому T ¹ 0 найти х, обеспечивающее выполнение условия

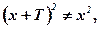
достаточно выбрать

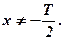
Таким образом, по любому Т такие хнаходятся (то есть существуют). Следовательно, функция 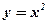не является периодической.

Это утверждение можно получить и более простым способом: функция 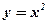обращается в ноль только тогда, когда х = 0, поэтому она не может быть периодической.

Заданные на всей действительной оси функции

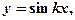
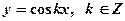
имеют период Т, вычисляемый по формуле

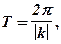
а функции

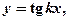
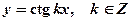
имеют период

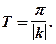
Если же, например, функция 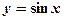задана на отрезке [0;1], то о её периодичности говорить не имеет смысла.

Не нужно думать, что периодическими функциями являются только тригонометрические.

Эта функция, вместе с тем, не имеет основного периода. Почему?

Так, функция Дирихле

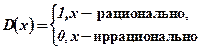периодическая (любое рациональное число будет ее периодом).

А вот функция

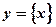(дробная часть числа x)

имеет период T = 1.

МОНОТОННОСТЬ ФУНКЦИИ.

Будем говорить, что функция 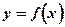является ВОЗ­РАСТАЮЩЕЙ (рис. 8.4, а) (УБЫВАЮЩЕЙ (рис. 8.4, б)) на некотором

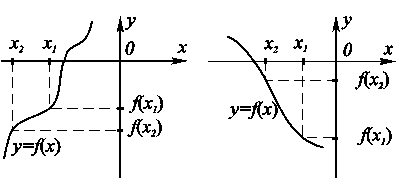a) б)   Рис. 8.4. Возрастающая и убывающая функции.

множестве Аиз области определения D(f), если большему значению аргумента из множества А соответствует большее (меньшее) значение функции.

f(x) –возрастает на множестве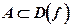

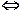
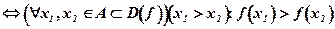, (8. 11)

( f(x)–убывает на множестве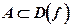

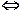
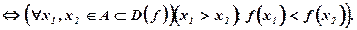(8. 12)

Рассматриваются также неубывающие (рис. 8.5, а) и невозрастающие функции (рис. 8.5, б).

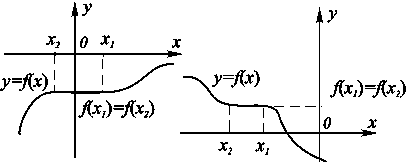а) б)   Рис. 8.5. Неубывающая и невозрастающая функции.

f(x) –неубывающая функция на множестве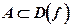

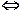
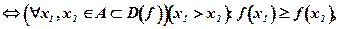(8. 13)

f(x) –невозрастающая функция на множестве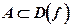

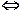
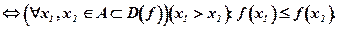(8. 14)

Возрастающие и убывающие функции называются СТРОГО МОНОТОННЫМИ; при условиях (8.13) и (8.14) монотонность является НЕСТРОГОЙ.

Рассмотрим отрицание какого-либо из утверждений (8.11) – (8.14), например (8.11) :

______

f(x) –возрастает на множестве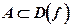

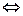
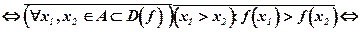
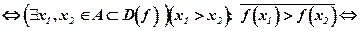
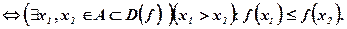
Сравнивая с утверждением (8.14), обнаруживаем, что если f(x) не является возрастающей, то такую функцию нельзя считать только невозрастающей в .

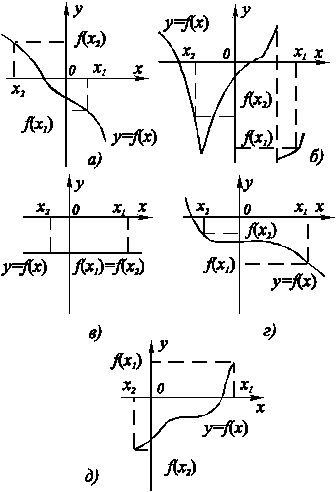
Возможны следующие случаи :

Рис. 8.6. Функции, не являющиеся возрастающими.

а) f(x) является убывающей (рис. 8.6, а).

б) f(x) не является монотонной (рис. 8.6, б).

в) f(x) = const (рис. 8.6, в).

г) f(x)является невозрастающей функцией (рис. 8.6, г).

д) f(x) неубывающая (рис. 8.6, д).