Статистическое определение вероятности

Событие и вероятность

Классический пример случайного события – подбрасывание монеты. Нельзя заранее предсказать, что выпадет – «орел» или «решка». Но если событие повторять многократно, подбрасывать монету тысячу, десятки тысяч раз, то относительная частота выпадения «орла» (отношение числа выпадений «орла» к общему числу подбрасываний) будет мало отличаться от 0,5 и чем больше число подбрасываний, тем ближе это отношение будет к 0,5.

Изучение закономерностей однородных массовых случайных явлений составляет предмет теории вероятностей и основанной на ней математической статистики.

Как и всякая математическая дисциплина теория вероятностей базируется на определенной аксиоматике и фактически является наукой о количественных закономерностях моделей случайных явлений независимо от их конкретной природы.

Сформулируем основные понятия и определения (будем обозначать символом Ñ):

Ñ Испытание – выполнение определенного комплекса условий при проведении какого-либо наблюдения или опыта.

Примеры(будем обозначать · ):

·Подбрасывание монеты и выпадение при этом «орла» или «решки»;

- подбрасывание игрального кубика и выпадение кверху одной из шести граней (от 1 до 6 очков);

- при определении жира в молоке, испытание – взятие пробы, лабораторный анализ.

Будем предполагать, что испытание может быть воспроизведено сколь угодно много раз.

Ñ Событие – результат, исход испытания.

· Выпадение «орла» или «решки» при подбрасывании монеты;

- выпадение конкретного числа очков при брошенной игральной кости.

Для обозначения событий будем использовать большие буквы латинского алфавита:
А, В, С, …

Ñ Два события А и В называются несовместимыми, если при одном испытании появление одного из них исключает появление другого.

· При подбрасывании монеты, события:

А = {выпадение «орла»} и В = {выпадение «решки»} - несовместимы;

- При одном выстреле по мишени, события:

А = {попадание} и В = {промах} - несовместимы.

Ñ События А и В – совместимы, если при испытании появление одного из них не исключает появление другого.

· При подбрасывании игрального кубика, события:

А = {выпадение четного числа очков} и

В = {выпадение числа очков, кратного «4»} - совместимы.

Ñ Событие называется достоверным, если оно является единственно возможным исходом испытания и невозможным, если в данном испытании оно заведомо не может произойти.

· В урне, т. е. ящике, из которого не видно что достаем, помещено пять белых шаров.

Событие А = {достать белый шар} - достоверное,

Событие В = {достать черный шар} - невозможное.

Ñ Событие называется случайным, если при испытании оно может либо произойти, либо не произойти.

· Извлечение белого шара из урны с 10 шарами, среди которых 5 белых и 5 черных шаров.

Ñ Возможные, исключающие дуг друга результаты одного испытания, будем называть элементарными событиями.

· При подбрасывании игрального кубика, события:

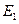= {выпадение 1 очка },

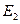= {выпадение 2 очков },

…….

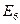= {выпадение 6 очков } - элементарные события.

В данном примере события 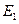, , 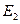… 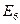образуют полную группу событий, так как они исчерпывают все возможные элементарные исходы.

Ñ События А и В называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.

· При подбрасывании монеты, события: А= {выпадение «орла»} и

В= {выпадение «решки»} - противоположны. Обозначают В = 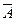(не А).

При подбрасывании игрального кубика, если А= {выпадение четного числа очков}, то 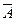= {выпадение нечетного числа очков} - противоположно А.

Статистическое определение вероятности

Предположим, что производится n испытаний и при этом некоторое событие А наступает m раз.

Ñ Число m называется абсолютной частотой ( или просто частотой) события А, а отношение m/n – относительной частотой события А.

· Пусть монету подбрасывают 100 раз и при этом «орел» выпадает 48 раз. Тогда 48 – абсолютная частота, а 0,48 – относительная частота выпадения «орла».

Ñ Если при сериях небольшого количества испытаний относительная частота может подвергаться значительным колебаниям, то при переходе к серии более многочисленных испытаний эти колебания постепенно сглаживаются и стабилизируются на каком-то устойчивом уровне.

Эти предельные стационарные значения относительной частоты в серии многочисленных одинаковых испытаний будем называть вероятностью наблюдаемого события А.

Статистическое определение вероятности, т.е. вероятность – как предельное значение относительной частоты при неограниченном увеличении количества испытаний, можно использовать для установления эмпирических закономерностей наблюдаемых явлений. Классический пример – опыты Менделя. Он скрещивал, например, два сорта гороха, различавшихся высотой растений, один сорт с высокими растениями, другой – с низкими. В первом поколении потомство состояло только из высоких растений (доминантный признак). А во втором поколении (при самоопылении гетерозигот) появлялись как высокие, так и низкие растения, но первых (доминант) было гораздо больше. На большом количестве опытов скрещивания (порядка десятков тысяч) выявилась числовая закономерность, что отношение доминантных признаков к рецессивным, при скрещивании гетерозигот, подчиняется пропорции 3 : 1. Полученная закономерность позволила Менделю высказать определенные гипотезы относительно механизмов скрещивания, которые, найдя подтверждение в опытах последующих исследователей, дошли до нас в виде законов Менделя.