Начальные и центральные теоретические моменты
Начальным моментом порядка k случайной величины X называют математическое ожидание величины Xk:
Найдем начальный момент первого порядка (k=1):
т.е. начальный момент первого порядка случайной величины X – это ее математическое ожидание.
Найдем начальный момент второго порядка (k=2):
т.о. начальный момент второго порядка случайной величины X – математическое ожидание случайной величины X2. Учитывая выражение (5.4) и полученные соотношения, можно выразить дисперсию случайной величины Xчерез ее начальные моменты:
(5.7)
Центральным моментом порядка k случайной величины X называют математическое ожидание величины
Найдем центральный момент первого порядка (k=1):
по свойству 5 математического ожидания.
Найдем центральный момент второго порядка (k=2):
согласно выражению (5.3).
Сопоставление последнего соотношения и (5.7) позволяет получить связь между начальными и центральными моментами случайной величины X:
Законы распределения
Для дискретных:
1 . Равномерное распределение
Так называют распределение случайной величины, которая может принимать любые значения в интервале (a,b), причем вероятность попадания ее в любой отрезок внутри (a,b) пропорциональна длине отрезка и не зависит от его положения, а вероятность значений вне (a,b) равна 0.
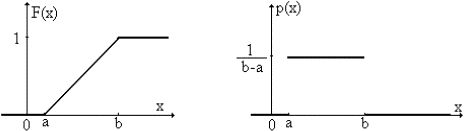
Рис 6.1 Функция и плотность равномерного распределения
Параметры распределения: a , b
2 . Нормальное распределение
Распределение с плотностью, описываемой формулой
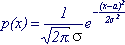 (6.1)
(6.1)
называется нормальным. (Рисунок 6.2)
Параметры распределения: a , σ
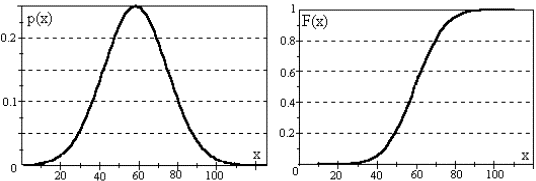
Рисунок 6.2 Типичный вид плотности и функции нормального распределения
3 . Распределение Бернулли
Если производится серия независимых испытаний, в каждом из который событие А может появиться с одинаковой вероятностью р, то число появлений события есть случайная величина, распределенная по закону Бернулли, или по биномиальному закону (другое название распределения).
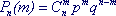 (6.2)
(6.2)
Здесь n - число испытаний в серии, m - случайная величина (число появлений события А), Рn(m) - вероятность того, что А произойдет именно m раз, q = 1 - р (вероятность того, что А не появится в испытании).
Пример 1: Кость бросают 5 раз, какова вероятность того, что 6 очков выпадет дважды ?
n = 5, m = 2, p = 1/6, q = 5/6
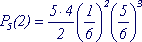
Параметры распределения: n , р
4 . Распределение Пуассона
Распределение Пуассона получается как предельный случай распределения Бернулли, если устремить р к нулю, а n к бесконечности, но так, чтобы их произведение оставалось постоянным: nр = а. Формально такой предельный переход приводит к формуле
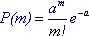 (6.3)
(6.3)
Параметр распределения: a
Распределению Пуассона подчиняются очень многие случайные величины, встречающиеся в науке и практической жизни.
Пример 2: число вызовов, поступающих на станцию скорой помощи в течение часа.
Разобьем интервал времени Т (1 час) на малые интервалы dt, такие что вероятность поступления двух и более вызовов в течение dt пренебрежимо мала, а вероятность одного вызова р пропорциональна dt: р = μdt ;
будем рассматривать наблюдение в течение моментов dt как независимые испытания, число таких испытаний за время Т: n = T / dt;
если предполагать, что вероятности поступления вызовов не меняются в течение часа, то полное число вызовов подчиняется закону Бернулли с параметрами: n = T / dt, р = μdt . Устремив dt к нулю, получим, что n стремится к бесконечности, а произведение n×р остается постоянным: а = n×р = μТ.
Пример 3: число молекул идеального газа в некотором фиксированном объеме V.
Разобьем объем V на малые объемы dV такие, что вероятность нахождения двух и более молекул в dV пренебрежимо мала, а вероятность нахождения одной молекулы пропорциональна dV: р = μdV; будем рассматривать наблюдение каждого объемчика dV как независимое испытание, число таких испытаний n=V/dV; если предполагать, что вероятности нахождения молекулы в любом месте внутри V одинаковы, полное число молекул в объеме V подчиняется закону Бернулли с параметрами: n = V / dV, р = μdV. Устремив dV к нулю, получим, что n стремится к бесконечности, а произведение n×р остается постоянным: а = n×р =μV.
