Моделирование непрерывной случайной величины

Непрерывная случайная величина 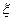определяется плотностью распределения вероятностей

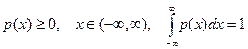, (1.3)

или функцией распределения

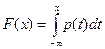, (1.4)

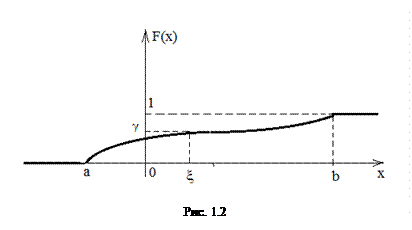
которая является строго монотонно возрастающей функцией и имеет свойства

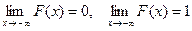. (1.5)

Вероятность попадания случайной величины 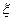с плотностью распределения вероятностей (1.3) в заданный интервал 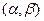равна

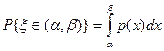(1.6)

или

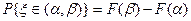. (1.7)

Если случайная величина 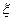определена в интервале 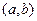, тогда

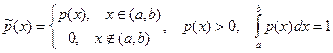, (1.8)

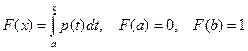. (1.9)

Теорема 1.2. Случайная величина 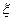, определённая на 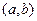и удовлетворяющая уравнению

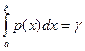(1.10)

или

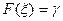, (1.11)

где 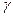равномерно распределённая на промежутке (0,1) случайная величина, имеет плотность распределения .

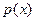Доказательство. Так как функция 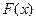строго монотонно возрастающая функция на промежутке 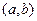, то уравнение (1.11) имеет при каждом 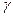единственный корень. Следовательно,

.

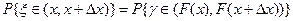Из того, что 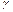равномерно распределена на промежутке (0,1) следует

,

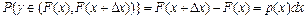что и требовалось доказать.

Замечание. Если возможно аналитическое вычисление интеграла, входящего в (1.10), то для определения 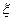получаем трансцендентное, вообще говоря, уравнение. Только в каждом частном случае для определённого 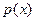можно утверждать или нет об эффективном способе решения полученного уравнения.

Пример 1.2. Найти формулу для моделирования случайной величины 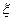, равномерно распределённой в интервале 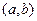. В этом случае плотность имеет вид

.

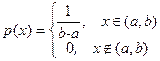Это распределение полностью определяется параметрами 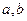, которые являются концами интервала определения случайной величины.

Чтобы получить формулу моделирования требуется решить уравнение (1.10). Для данного примера имеем

.

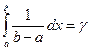Откуда получаем

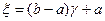. (1.12)

Здесь 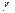– равномерно распределённая на (0,1) случайная величина.

Замечание.Если требуется получить случайный вектор 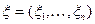, равномерно распределённый в параллелепипеде 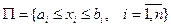, то нужно использовать формулу (1.12) для получения каждой координаты при 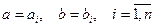, а именно

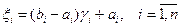, (1.13)

где 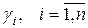– независимые реализации .

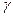§1.3. Алгоритм получения случайной равномерно распределённой точки в заданной области

Введём параллелепипед 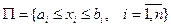, включающий область 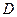. Требуется получить 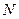реализаций случайного равномерно распределённого в области 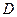вектора .

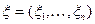1. Пусть .
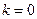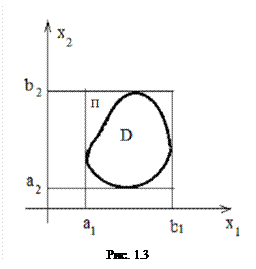2. Получим по формуле (1.13) реализацию случайного равномерно распределённого в параллелепипеде 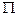вектора .
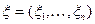3. Если 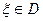, то мы получили искомый вектор и посчитаем эту точку: 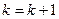. Если 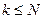то возвращаемся в пункт 2). В противном случае, когда все точки получены и можно заканчивать процедуру получения точек, идем в пункт 5).
4. Если 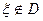, то идти в пункт 2).
5. Конец процедуры.

Пример 1.3. Найти формулу для моделирования случайной величины 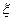, распределённой по закону Релея

,

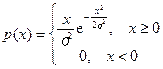где 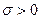параметр распределения.

Для получения формулы моделирования требуется решить уравнение

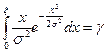
относительно 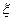. Для этого вычислим сначала интеграл, сделав замену переменной

.

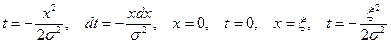
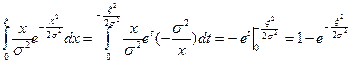Имеем следующее уравнение для :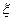

,

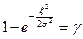откуда получаем

.

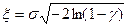Величина 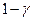распределена так же, как и 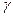, поэтому можно упростить полученную формулу

.

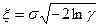Заметим, что .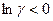

Пример 1.4. Случайная величина 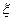определена в интервале 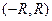с плотностью

.

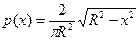Запишем уравнение (1.10) для нахождения формулы моделирования заданной случайной величины

.

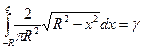Вычислив интеграл, получаем уравнение относительно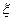

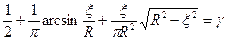. (1.14)

Из этого уравнения 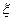явно не выражается.