Расчет толстостенной трубы
При нагружении трубы внутренним или внешним давлениями пластические деформации появляются в точках внутренней поверхности и поэтому пластической является кольцевая область радиуса rt, примыкающая к отверстию.
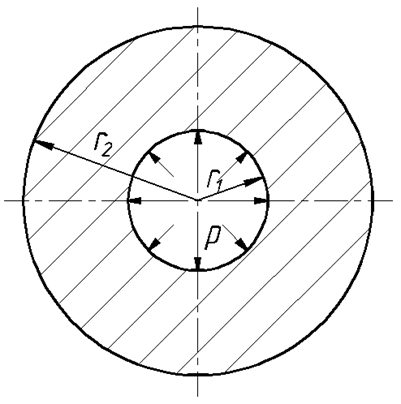
В упругой области радиальные σr и окружные σt напряжения определяются по формулам: 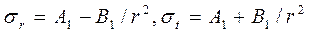 , которые удобно записывать в виде:
, которые удобно записывать в виде:
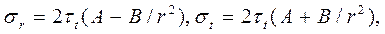 (1)
(1)
где τt – предел текучести при сдвиге.
 По условию задачи
По условию задачи
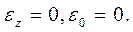 (2)
(2)
Здесь ε0 - объемная деформация.
На основании обобщенного закона Гука с учетом (2) получаем зависимость между напряжениями:
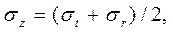 (3)
(3)
которая справедлива и за пределами упругости. Это можно показать, используя соотношения между напряжениями и деформациями за пределами упругости.
Определим напряжения в пластической области. Уравнение равновесия элемента трубы имеет вид
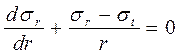 . (4)
. (4)
Разность напряжений во втором слагаемом пропорциональна интенсивности напряжений, которая в данной задаче равна
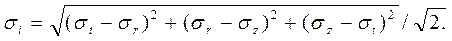
 Подставляя в это соотношение выражение σz и учитывая, что интенсивность напряжений – величина положительная, получим σi=√3*|σt-σr|/2. Так как разность σt-σr может иметь различный знак, то последнее удобно представить в виде
Подставляя в это соотношение выражение σz и учитывая, что интенсивность напряжений – величина положительная, получим σi=√3*|σt-σr|/2. Так как разность σt-σr может иметь различный знак, то последнее удобно представить в виде
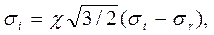 (5)
(5)
где χ=±1, причем знак определяется условиями нагружения.
Подставив в уравнение равновесия (4) разность напряжений согласно выражению (5), получим
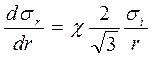 . (6)
. (6)
Чтобы проинтегрировать уравнение (6), необходимо иметь зависимость интенсивности напряжений от радиуса. Для этого установим сначала зависимость интенсивности деформаций
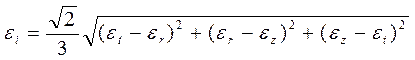 (7)
(7)
от радиуса.
Деформации и радиальное перемещение связаны соотношениями:
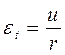 ,
, 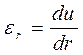 (8)
(8)
Из условия несжимаемости и равенства нулю осевой деформации (2) следует дифференциальное уравнение для радиального перемещения
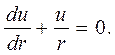
Интеграл имеет вид
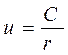 . (9)
. (9)
Из соотношений (8) и (9) получаем выражения для деформаций:
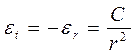 , (10)
, (10)
а из выражения (7):
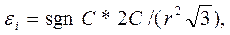 (11)
(11)
где sgn C – знак постоянной С.
Используя соотношение между деформациями и напряжениями и равенства (2) и (3), получаем 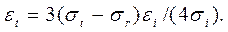 Подставив σi, εt и εi по формулам (5),(10) и (11) устанавливаем, что знак χ совпадает со знаком постоянной С, т.е. χ=1sgnC. Введем для удобства новую постоянную С1
Подставив σi, εt и εi по формулам (5),(10) и (11) устанавливаем, что знак χ совпадает со знаком постоянной С, т.е. χ=1sgnC. Введем для удобства новую постоянную С1
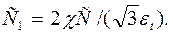 (12)
(12)
 Тогда зависимость интенсивности деформаций от радиуса принимает вид
Тогда зависимость интенсивности деформаций от радиуса принимает вид
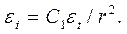 (13)
(13)
Подставив это выражение в уравнение закона упрочнения, устанавливаем зависимость интенсивности напряжений от радиуса
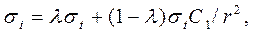 (14)
(14)
что позволяет после интегрирования уравнения (6) получить выражения для радиальных напряжений
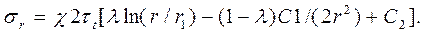 (15)
(15)
Из соотношений (5), (14) и (15) устанавливаем формулу для окружных напряжений
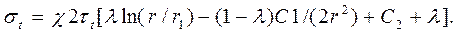 (16)
(16)
Постоянные А, В, С1, С2и радиус rT определяются из граничных условий:
при 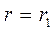
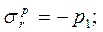
при 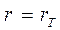
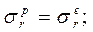
при 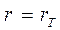
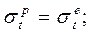
при r = rT 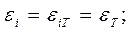
при 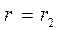
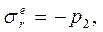
где индексами e и p отмечены напряжения соответственно в упругой и пластической областях.
Из четвертого граничного условия:

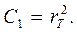 (17)
(17)
Вместо условия непрерывности окружных напряжений удобнее использовать условие равенства эквивалентного напряжения пределу текучести на границе
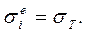 (18)
(18)
 В силу равенства (5) и второго граничного условия окружные напряжения при r=rT остаются непрерывными. Из равенства (18) получаем
В силу равенства (5) и второго граничного условия окружные напряжения при r=rT остаются непрерывными. Из равенства (18) получаем 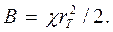 Из пятого граничного условия:
Из пятого граничного условия:
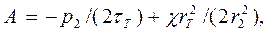
а из первого – постоянную С2
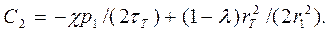
Подставляя найденные значения постоянных A, B, C1, C2 во второе граничное условие, получаем уравнение, связывающее радиус rT и давление p1 и p2:
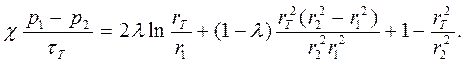 (19)
(19)
Отсюда устанавливаем зависимость знака χ от внешней нагрузки. Выражение, стоящее в правой части, положительно, так как λ≤1, r2>r1 и r1≤rT≤r2. Знак определяется знаком разности давлений, т.е.
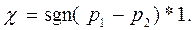 (20)
(20)
Подставив в выражения (15) и (16) значения постоянны С1 и С2 и используя условие (3), получим формулы для напряжений в пластической области:
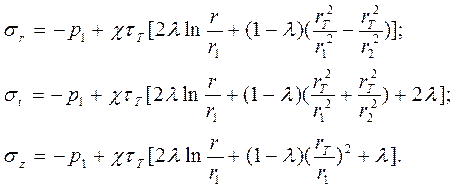 (21)
(21)
Формулы для напряжений в упругой области выводим, подставив значения постоянных А и В в выражения (1) и учитывая равенство (3):
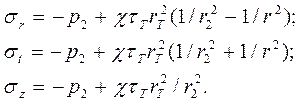 (22)
(22)
Найдем осевую силу N, которая связана с осевыми напряжениями σz соотношением
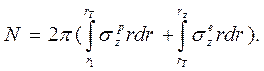
Подставим в него выражения напряжений σz согласно формулам (21) и (22). Получаем 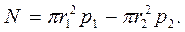
Таким образом, для того чтобы осевая деформация была равна нулю, к торцу толстостенной трубы должна быть приложена осевая сила, равная равнодействующей сил внешнего и внутреннего давлений на днище.
Определим радиальное перемещение. Из соотношения (9), учитывая равенство (12) и (17), имеем 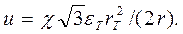 Это выражение справедливо для упругой и пластической областей.
Это выражение справедливо для упругой и пластической областей.
Посчитаем внутреннее давление. Поскольку p1>p2, то на основании (20) устанавливаем, что χ=+1. Из формулы (19) находим p1=1,46σT=1170 МПа.
