Урок № 77. Тема 9.3. Пирамида

План занятия.

D

A

B

C

P

H

O

1) Определение многогранного угла.

2) Определение пирамиды.

3) Элементы пирамиды.

4) Формула боковой поверхности пирамиды.

5) Виды пирамиды.

Определение. Пирамидой называется многогранник, образованный всеми отрезками, соединяющими данную точку – вершину пирамиды с точками плоского многогранника - основания пирамиды.

Определение. Усеченной пирамидой называется часть пирамиды, заключенная между ее основанием и секущей плоскостью параллельной основанию.

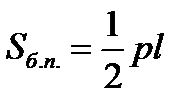
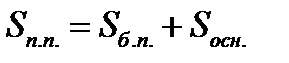
Решение задачи.

Задача. В правильной треугольной пирамиды сторона основания равна 8 см, а боковое ребро составляет с плоскостью основания угол 60⁰. Определить Sполн.

Ответ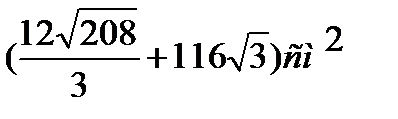

Итоговые вопросы:

1. Определение пирамид.

2. Виды пирамид.

3. Назовите элементы пирамиды.

Домашнее задание

1. Выучить содержание конспекта.
2. Задача 1. В правильной четырехугольной пирамиде сторона основания равна 8 см, а боковая грань образует с плоскостью основания угол 60⁰. Определить Sполн.

Ответ 192 см².

1. Задача №2. Основание пирамиды прямоугольник со сторонами 6 см и 8 см, каждое боковое ребро равно 13см. Определить высоту. Ответ 12 см.

Урок № 78 (2) Тема: Усеченная пирамида.

План.

1. Дать определение усеченной пирамиды. Назвать элементы усеченной пирамиды.

2. Доказать теорему о S бок. правильной усеченной пирамиды.

Определение. Пирамидой называется многогранник , одна из граней которого многоугольник, а остальные грани-треугольники , имеющие общую вершину.

Если основание пирамиды –правильный многоугольник и вершина пирамиды проектируется в центр этого многоугольника, то пирамиду называют правильной.

Сечение пирамиды плоскостью, параллельной ее основанию, можно отобразить на основание гомотетией с центром в вершине пирамиды.

Усеченная пирамида имеет два основания, являющиеся гомотетичными многоугольниками.

Перпендикуляр к плоскостям оснований усеченной пирамиды, концы которого принадлежат этим плоскостям, называют высотой усеченной пирамиды.

Боковые грани правильной усеченной пирамиды- конгруэнтные равнобедренные трапеции, их высоты называют апофемами усеченной пирамиды.

Площадь боковой поверхности правильной усеченной пирамиды равна полусумме периметров, оснований, умноженной на апофему.

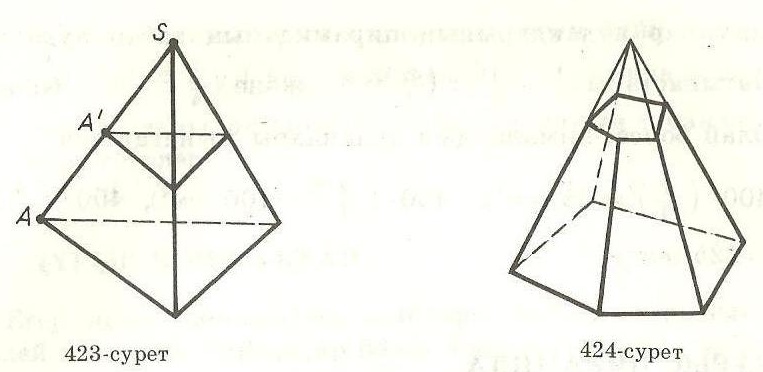
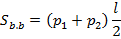
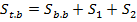
3. Решение задачи.

Задача №1. Определить Sбок. правильной четырехугольной усеченной пирамиды, если диагонали оснований 8 см и 4 см, а боковое ребро равно 12 см. Ответ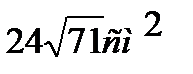

Задача №2. Определить Sполн. Правильной усеченной треугольной пирамиды со сторонами 4 см и 2 см, а апофема наклонена к плоскости основания под углом 45⁰.

Ответ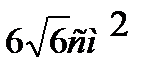

Домашнее задание

а) Изучить конспект.

б) Задача №1. В правильной четырехугольной усеченной пирамиде стороны оснований 8м и 2м. Высота равна 4м. Найти Sп. Ответ 168м².

Задача №2. Стороны оснований правильной усеченной треугольной пирамиды 6м и 12м, высота равна 1м. Найти Sб. Ответ 54м².