Преобразования движения в механизме
Рассматривается механизм с одной степенью подвижности  , с вращающимся входным звеном, угол
, с вращающимся входным звеном, угол 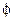 есть обобщенная координата механизма (1.3).
есть обобщенная координата механизма (1.3).
Сейчас мы поставим ограниченную задачу: определить, как движение входного звена преобразуется в движение других звеньев механизма. При этом конкретный вид функции 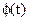 нам не важен.
нам не важен.
Положение звеньев механизма зависит лишь от его обобщенной координаты, поэтому для звена номер  и точки
и точки  на нем можно записать
на нем можно записать
 (2.1)
(2.1)
 (2.2)
(2.2)
здесь 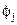 - угол поворота
- угол поворота  -го звена;
-го звена;  - радиус-вектор точки
- радиус-вектор точки  в выбранной системе координат.
в выбранной системе координат.
Функции (2.1), (2.2) есть функции положения. Дифференцируя их по времени с учетом (1.3), получим выражения для угловой скорости 
 -го звена и скорости
-го звена и скорости  точки
точки  :
:
 , (2.3)
, (2.3)
 ; (2.4)
; (2.4)
здесь  - обобщенная угловая скорость механизма.
- обобщенная угловая скорость механизма.
Для определения углового ускорения 
 -го звена и ускорения
-го звена и ускорения  точки
точки  продифференцируем по времени скорости (2.3) и (2.4):
продифференцируем по времени скорости (2.3) и (2.4):
 , (2.5)
, (2.5)
 ; (2.6)
; (2.6)
здесь  - обобщенное угловое ускорение механизма.
- обобщенное угловое ускорение механизма.
Входящие в выражения (2.3)-(2.6) производные 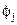 и
и  по обобщенной координате
по обобщенной координате 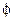 носят названия аналогов скоростей и ускорений:
носят названия аналогов скоростей и ускорений:
 -аналог угловой скорости;
-аналог угловой скорости;  - аналог углового ускорения;
- аналог углового ускорения;
 -аналог линейной скорости;
-аналог линейной скорости;  -аналог линейного ускорения.
-аналог линейного ускорения.
Размерность аналогов определяется размерностью обобщенной координаты. Еслиобобщенная координата есть угол поворота, то аналоги угловой скорости и углового ускорения, как следует из (2.3), (2.5), безразмерны, а аналоги линейной скорости и линейного ускорения (2.4), (2.6) имеют размерность длины. При выборе в качестве обобщенной другой координаты, не являющейся углом, размерности аналогов изменятся — их в этом случае следует поделить на размерность новой обобщенной координаты. В любом случае аналоги являются относительными величинами. Отметим, что аналоги численно равны скоростям и ускорениям, если  ,
,  .
.
Конкретный вид функций положения (2.1) и (2.2) и аналогов (2.3)-(2.6) определяется строением механизма и размерами звеньев; эти функции являются геометрическими характеристиками преобразования движения в механизме.
Определение перечисленных характеристик механизма является целью кинематического анализа и составляет содержание его трех основных задач.
Задача о положениях состоит в определении функций положения вида (2.1), (2.2); задача о скоростях заключается в отыскании функций линейных и угловых скоростей (2.3), (2.4) (или только их аналогов  ,
,  ); задача об ускорениях сводится к нахождению функций (2.5), (2.6) (или только аналогов
); задача об ускорениях сводится к нахождению функций (2.5), (2.6) (или только аналогов  ,
,  ).
).
Основной и наиболее сложной является первая из этих задач — задача о положениях; аналитически она обычно описывается нелинейными уравнениями. Решение двух других задач сводится к дифференцированию функций положения, которое может быть выполнено с использованием стандартных процедур дифференцирования в среде Mathcad.
Зная закон движения входного звена в реальном времени, можно пересчитать геометрические аналоги кинематических величин, полученные на первом этапе, в истинные скорости и ускорения (линейные и угловые) интересующих нас точек и звеньев механизма по формулам (2.3)-(2.6).
Для использования этих формул необходимо обобщенную угловую скорость  и обобщенное угловое ускорение
и обобщенное угловое ускорение  выразить через заданные
выразить через заданные 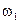 и
и 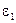 . С этой целью рассмотрим кинематику входного звена механизма.
. С этой целью рассмотрим кинематику входного звена механизма.
Кинематика входного звена механизма.
 Введем функцию углового положения
Введем функцию углового положения 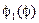 входного звена, учитывающую заданное
входного звена, учитывающую заданное
направление его вращения в составе механизма:
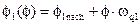 , где
, где
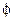 - обобщенная координата механизма (1.3);
- обобщенная координата механизма (1.3);
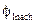 - угол, соответствующий задаваемому начальному положению входного звена;
- угол, соответствующий задаваемому начальному положению входного звена;  - аналог угловой скорости входного
- аналог угловой скорости входного
Рис. 2. звена. Очевидно,  равняется
равняется  или
или  , аналог углового ускорения
, аналог углового ускорения  . Используя формулы (2.3) и (2.5), получим выражение для обобщенной скорости
. Используя формулы (2.3) и (2.5), получим выражение для обобщенной скорости  и обобщенного ускорения
и обобщенного ускорения  или, что то же самое,
или, что то же самое,  ,
,  .
.
