Тема 4. Модели краткосрочного страхования жизни

Задача 4.1. Предположим, что в компании застраховано 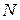= 3000 человек с вероятностью смерти в течение года 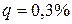. Компания выплачивает сумму 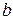= 250000 руб. в случае смерти застрахованного в течение года и не платит ничего, если этот человек доживет до конца года. Определите величину активов, достаточную, чтобы обеспечить вероятность разорения порядка 5%.

Решение.

Примем размер страховой суммы в качестве новой денежной единицы.

Прежде всего, мы должны подсчитать среднее значение и дисперсию суммарного ущерба .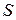

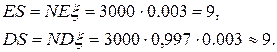
Поэтому

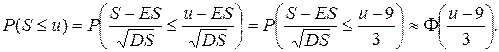
Если мы хотим, чтобы вероятность разорения была 5%, величина 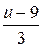должна быть равной 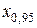= 1,645, т.е. 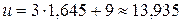(от величины страхового пособия) или в абсолютных цифрах около 3 483 750 руб.

Задача 4.2. Предположим, что страховая компания заключила 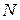= 10000 договоров страхования жизни сроком на один год на следующих условиях: в случае смерти застрахованного в течение года от несчастного случая компания выплачивает наследникам 1000000 руб., а в случае смерти в течение года от естественных причин компания выплачивает наследникам 250000 руб. Компания не платит ничего, если застрахованный не умрет в течение года. Вероятность смерти от несчастного случая одна и та же для всех застрахованных и равна 0.0005. Вероятность смерти от естественных причин зависит от возраста. В первом приближении можно разбить 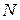застрахованных на две возрастные группы, содержащие 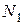= 4000 и 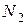= 6000 человек с вероятностью смерти в течение года 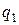= 0.004 и 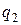= 0.002 соответственно.

Подсчитайте величину премии, гарантирующую вероятность выполнения компанией своих обязательств, равную 95%.

Решение.

Примем сумму 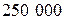руб. в качестве единицы измерения денежных сумм. Тогда для первой группы договоров индивидуальный убыток принимает три значения: 0, 1 и 4 с вероятностями 0.9955, 0.0040 и 0.0005 соответственно:

0,9955	0,004	0,0005

Среднее значение и дисперсия величины индивидуального убытка для первой группы застрахованных есть

,

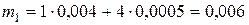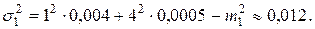
Для второй группы договоров индивидуальный убыток принимает те же три значения 0,1 и 4, но с другими вероятностями: 0,9975, 0,002 и 0,0005:

0,9975	0,002	0,0005

В этой группе среднее значение и дисперсия индивидуального убытка есть

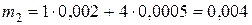
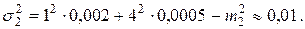
Среднее значение и дисперсия суммарного убытка равны:

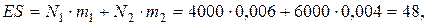
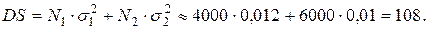
Для того, чтобы гарантировать 95% вероятность неразорения, резервный фонд компании должен быть равен 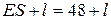, где добавочная сумма 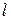определяется по формуле

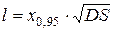
и в нашем случае будет равна

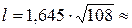
Рассмотрим теперь вопрос о назначении индивидуальных премий.

I. Если добавочная сумма 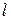делится пропорционально нетто-премиям, то в соответствии с (6.5.3) относительная страховая надбавка 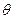одна и та же для всех договоров и равна

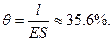
Поэтому для договоров из первой группы премия равна

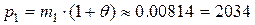руб.

Для договоров из второй группы премия равна

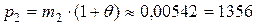руб.

II. Если добавочная сумма 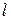делится пропорционально дисперсиям, то коэффициент пропорциональности 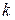есть

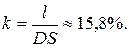
Поэтому для договоров из первой группы страховая надбавка равна

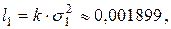
так что премия есть

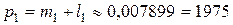руб.

а относительная страховая надбавка

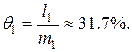
Для договоров из второй группы страховая надбавка равна

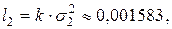
так что премия есть

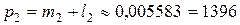руб.

а относительная страховая надбавка

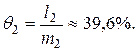
III. Если добавочная сумма 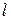делится пропорционально средним квдратическим отклонением (они равны 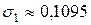для договоров первой группы и 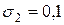для договоров второй группы), то коэффициент пропорциональности 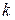есть

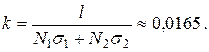
Поэтому для договоров из первой группы страховая надбавка равна

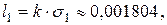
так что премия есть

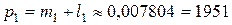руб.

а относительная страховая надбавка

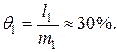
Для договоров из второй группы страховая надбавка равна

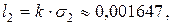
так что премия есть

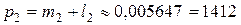руб.

а относительная страховая надбавка

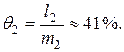
Итак, изменение принципа назначения индивидуальных премий приводит к уменьшению относительной страховой надбавки для договоров первой группы: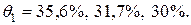

Соответственно для договоров второй группы относительная защитная надбавка увеличивается: 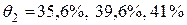. Это связано с тем, что коэффициент рассеяния суммарного ущерба есть

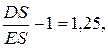
в то время как для договоров первой (второй) группы он равен 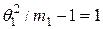(соответственно 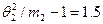). Коэффициент вариации величины индивидуального убытка для договоров первой группы есть

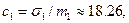
а для договоров второй группы он равен

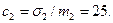
Средний коэффициент вариации, усредненный по всему портфелю с весами 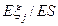, есть

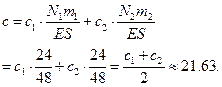
Задача 4.3. Страховая компания предлагает договоры страхования жизни на один год. Информация относительно структуры покрытия приведена в следующей таблице:

Страховая сумма	Причина смерти	Вероятность
500 000	Обычная	0,1
1 000 000	Несчастный случай	0,01

Относительная защитная надбавка равна 20%.

Предположим, что отдельные полисы независимы и страховщик использует нормальное приближение для распределения суммарных выплат.

Сколько договоров должен продать страховщик, чтобы собранная премия с вероятностью 95% покрывала суммарные выплаты?

Решение.

Пусть 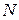– общее число проданных договоров. 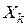– выплаты по 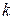-му договору, 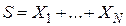– суммарные выплаты по всему портфелю, 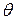– относительная защитная надбавка, так что премия по одному договору равна .

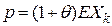По условию, 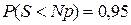. С другой стороны,

.

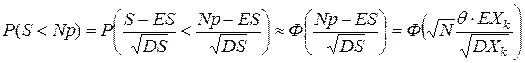Поэтому

,

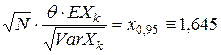где 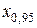– квантиль порядка 0,95 стандартного нормального (гауссовского) распределения.

Отсюда для искомого числа договоров имеем:

.

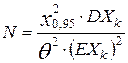Поскольку для индивидуального договора,

,

,

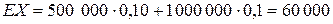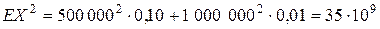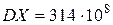, искомое число договоров равно 590.

Задача 4.4. Компания ABC предполагает организовать групповое страхование жизни для своих сотрудников. Структура персонала приведена в следующее таблице:

Профессиональный класс	Число сотрудников	Страховая сумма	Вероятность смерти
			0,1
			0,2
			0,1
			0,2

Компания ABC предполагает внести в страховой фонд сумму, равную ожидаемым выплатам страховых возмещений.

Каждый сотрудник, в свою очередь, должен будет внести сумму, равную определенной доле 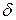от размера ожидаемой выплаты. Размер этой доли определяется таким образом, чтобы с вероятностью 95% средств страхового фонда хватило для выплаты страховых возмещений.

Определите размер взноса для работников четвертого профессионального класса.

Решение.

Пусть 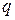– вероятность смерти сотрудника, 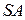– размер страховой суммы. Поскольку индивидуальные потери по договору принимают только два значения: 0 с вероятностью 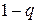и 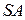с вероятностью 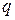, среднее значение индивидуальных потерь есть 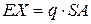, а дисперсия – .

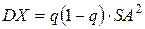Предполагая независимость времен жизни сотрудников компании, можно подсчитать среднее и дисперсию суммарных выплат для каждого профессионального класса. Для этого нужно среднее (соответственно дисперсию) индивидуальных потерь умножить на число работников в классе:

.

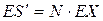
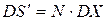Результаты расчетов поместим в таблицу:

Класс	Число Сотрудников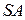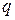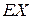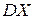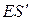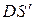
			0,1 0,2 0,1 0,2	0,1 0,2 0,2 0,4	0,09 0,16 0,36 0,64

Чтобы получить среднее значение (дисперсию) суммарных выплат 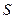для всего портфеля, нужно сложить средние (дисперсии) суммарных потерь для всех четырех профессиональных классов, так что

, .

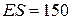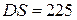Размер страхового фонда равен 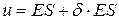. По условию, должно быть верно равенство

,

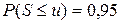или, что то же самое,

.

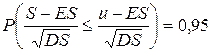Применяя гауссовское приближение для центрированной и нормированной величины общих выплат, мы имеем:

.

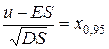В рассматриваемой ситуации это равенство примет вид:

.

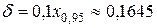Соответственно защитная надбавка для работников четвертого профессионального класса равна 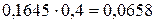. Иначе говоря, .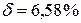