Граничные условия Леонтовича
1.Реальный проводник. Направим ось z в сторону («вглубь») проводника (рис 3-55). В этом случае «обобщенное» уравнение (146) для проводящей среды (среда 2) запишется со знаком минус при множителях, определяющих затухание волны 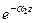 и направление распространении волны
и направление распространении волны 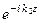 (направление волнового вектора k2)
(направление волнового вектора k2)
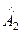 =
= 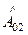
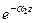
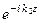 .
.
Запишем комплексные амплитуды для каждого из векторов E и Hв явном виде:
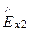 =
= 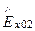
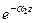
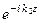 ,
, 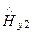 =
= 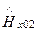
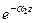
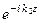 .
.
В этих уравнениях 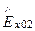 и
и 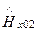 - комплексные амплитуды на границе раздела сред (индекс «0»). Вектор Пойнтинга П2 = [E2, H2] направлен в объем проводника, и энергия электромагнитного поля переходит во внутреннюю энергию проводника с выделением тепла.
- комплексные амплитуды на границе раздела сред (индекс «0»). Вектор Пойнтинга П2 = [E2, H2] направлен в объем проводника, и энергия электромагнитного поля переходит во внутреннюю энергию проводника с выделением тепла.
Компоненты векторовE и H в реальном проводнике определяются соотношениями (151) и (152)
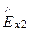 =
= 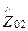
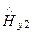 ,
,
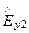 = -
= - 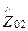
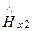
На границе раздела сред (z = 0) имеем соотношения
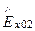 =
= 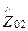
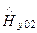 ,
,
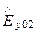 = -
= - 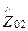
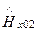
 В реальном проводнике с большой, но конечной проводимостью касательная составляющая
В реальном проводнике с большой, но конечной проводимостью касательная составляющая 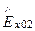 ¹ 0. Кроме того, из граничного условия для касательной составляющей имеем
¹ 0. Кроме того, из граничного условия для касательной составляющей имеем
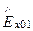 =
= 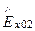 .
.
Несмотря на малость величины 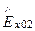 (волновое сопротивление
(волновое сопротивление 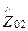 проводящей среды мало), касательная составляющая определяет поток электромагнитной энергии в объем проводника П2 с выделение тепла в проводнике.
проводящей среды мало), касательная составляющая определяет поток электромагнитной энергии в объем проводника П2 с выделение тепла в проводнике.
Коэффициент затухания в проводящей среде a2 имеет смысл обратной величины расстояния l0 , на которой амплитуда электромагнитной волны уменьшается в e = 2,7 раз. В проводящей среде a » 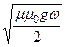 (§ 3.6.2, пункт 2.Б), поэтому
(§ 3.6.2, пункт 2.Б), поэтому
l0 = 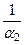 =
= 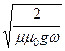 . (153)
. (153)
С ростом частоты w электромагнитной волны, проводимости g и магнитной проницаемости m проводника глубина проникновения l0 уменьшается. Например, при частоте f = 1МГц глубина проникновения электромагнитной волны в медь и серебро l0 » 6,5×10-5 м = 6,5×10-2 мм, а при частоте f = 1,6 ГГц l0 » 6,5×10-4 мм.
Плотность тока на поверхности проводника направлена по оси x и определяется законом Ома:
jx = g2 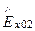
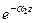
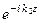 .
.
Таким образом, амплитуда тока убывает с глубиной проникновения электромагнитного поля по закону
újx0ê = úg2 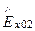 ê
ê 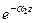 .
.
Это явление убывания тока называется поверхностным эффектом в проводниках в поле электромагнитной волны.
2.Идеальный проводник. Идеальным проводником считается среда, проводимость которой g = ¥ (удельное сопротивление r = 0). В соответствии с (153) глубина проникновения l0 = 0, и в объеме идеального проводника электромагнитная волна отсутствует(E2 = 0, H2 = 0).
Граничные условия для переменного магнитного поля на поверхности S проводника:
H 01t = j0S (т.к. H2 = 0),
где j0S - поверхностная плотность тока на единице Dx = 1м.
Граничные условия для переменного электрического поля на поверхности S проводника:
D01n = s или e1e0 E01n = s;
где s - плотность заряда на поверхности проводника.
Из граничных условий непосредственно следует, что на поверхности проводника E01t = 0; H01n = 0,
так как в идеальном проводнике электромагнитное поле отсутствует (E2t = 0, H2n = 0).
3.Приближенное граничные условия Леонтовича.Вернемся к рис. 3-55, где координатная плоскость x0y совпадает с плоскостью раздела сред. В проводящей среде угол преломления близок к нулю (f = 0). В этой связи, приближенно можно считать, что векторы E и H в этой среде имеют компоненты только по осям x и y:
Ex2 и Ey2; Hx2 и Hy2.
Компоненты векторовE и H в реальном проводнике на границе раздела сред определяются соотношениями
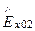 =
= 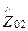
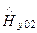 ,
,
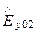 = -
= - 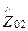
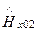
Приравнивая касательные составляющие, получим:
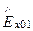 =
= 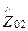
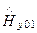 , (154)
, (154)
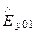 = -
= - 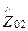
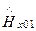 (155)
(155)
Соотношения (154) и (155) есть граничные условия Леонтовича, связывающие касательные составляющие векторов E и Hв первой среде (диэлектрике) с волновым сопротивлением второй среды (проводника). Условия Леонтовича позволяют, не определяя поле внутри проводника, приближенно учесть его влияние на поле в диэлектрике с помощью соотношений (154) и (155).
В случае идеального проводника H 01t = j0S. Приближенно считая, что реальная проводящая среда близка к идеальному проводнику, можно привести еще одну форму записи приближенного условия Леонтовича на границе раздела диэлектрик-проводник:
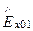 =
= 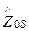
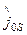 =
= 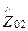
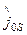 , (156)
, (156)
где 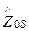 =
= 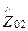 - поверхностное сопротивление проводника, т.к. в идеальном проводнике глубина проникновения волны l0 = 0.
- поверхностное сопротивление проводника, т.к. в идеальном проводнике глубина проникновения волны l0 = 0.
