Вращательное движение твёрдого тела вокруг неподвижной оси. Угловая скорость и угловое ускорение

Вращательное движение

- это такое движение, когда у тела имеется подмножество частиц, неподвижных во времени относительно какой-либо оси системы отсчёта. Такую ось называют осью вращения.

В рамках рассматриваемого подраздела ось вращения будем обозначать буквой 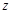, а её орт - 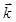. Примеры вращательных движений: ротор электродвигателя, карусель, дверь и т.п.

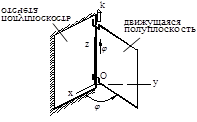
При описании вращательного движения полуплоскость системы отсчёта, начинающуюся с оси вращения, называют неподвижной полуплоскостью (или полуплоскостью отсчёта - см. рис.5).

Полуплоскость, начинающуюся с оси вращения и связанную с телом, называют подвижной полуплоскостью.

Об угловых скоростях и ускорениях

Процесс перемещения подвижной полуплоскости относительно неподвижной называют поворотом тела. Количественной его характеристикой является

угол поворота – это двухранный угол 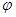между подвижной и неподвижной полуплоскостями, рассматриваемый как алгебраическая величина - больше нуля тогда, когда мысленное движение в направлении изображающей его круговой стрелки оказывается встречным по отношению к движению конца стрелки часов при условии, что циферблат виден с положительного направления оси вращения.

вектор поворота – это вектор, определяемый из математического выражения: .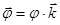

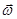18.10

угловая скорость ( ) – это кинематическая мера вращательного движения твёрдого тела, определяемая как первая производная по времени от вектора поворота, т.е.

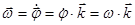, где

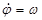- проекция угловой скорости на ось вращения.

Единицей измерения угловой скорости является радиан за секунду, что в записях обозначают: 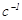, либо (редко) - .

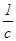В практике чаще частоту вращения оценивают числом оборотов в минуту ( 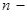об/мин). Т.к. за одну минуту тело поворачивается на 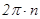радиан, а за секунду на угол в 60 раз меньший, то

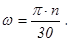угловая скорость тела (речь идёт о модуле 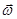), выраженная в радианах за секунду, с числом оборотов в минуту связана соотношением

Угловое ускорение ( 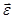) – это кинематическая мера вращательного движения твёрдого тела, определяемая как первая производная по времени от угловой скорости, т.е.

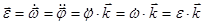, где

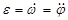- проекция углового ускорения на ось вращения.

Единицей измерения углового ускорения является .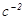

Подобно тому, как это делалось при рассмотрении кинематики точки,

принято различать:

если 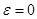, т.е. 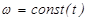- вращение равномерное;

если 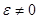- вращение переменное

(при - ускоренное; при 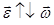- замедленное);

если 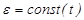- вращение равнопеременное

(при 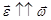- равноускоренное; при 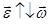- равнозамедленное).

Равномерное и равнопеременное вращение.