Что такое однородная система линейных уравнений?

Однородные системы линейных алгебраических уравнений

В рамках уроков метод Гаусса и Несовместные системы/системы с общим решениеммы рассматривали неоднородные системы линейных уравнений, где свободный член(который обычно находится справа) хотя бы одного из уравнений был отличен от нуля.
И сейчас, после хорошей разминки с рангом матрицы, мы продолжим шлифовать техникуэлементарных преобразований на однородной системе линейных уравнений.
По первым абзацам материал может показаться скучным и заурядным, однако данное впечатление обманчиво. Помимо дальнейшей отработки технических приёмов будет много новой информации, поэтому, пожалуйста, постарайтесь не пренебрегать примерами данной статьи.

Что такое однородная система линейных уравнений?

Ответ напрашивается сам собой. Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например:

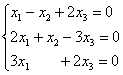
Совершенно ясно, что однородная система всегда совместна, то есть всегда имеет решение. И, прежде всего, в глаза бросается так называемое тривиальное решение 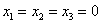. Тривиальное, для тех, кто совсем не понял смысл прилагательного, значит, беспонтовое. Не академично, конечно, но зато доходчиво =) …Чего ходить вокруг да около, давайте выясним, нет ли у данной системы каких-нибудь других решений:

Пример 1

Решить однородную систему линейных уравнений

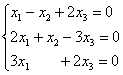
Решение: чтобы решить однородную систему необходимо записать матрицу системы и с помощью элементарных преобразований привести её к ступенчатому виду. Обратите внимание, что здесь отпадает необходимость записывать вертикальную черту и нулевой столбец свободных членов – ведь что ни делай с нулями, они так и останутся нулями:

(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3.

(2) К третьей строке прибавили вторую строку, умноженную на –1.

Делить третью строку на 3 не имеет особого смысла.

В результате элементарных преобразований получена эквивалентная однородная система 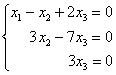, и, применяя обратный ход метода Гаусса, легко убедиться, что решение единственно.

Ответ: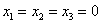

Сформулируем очевидный критерий: однородная система линейных уравнений имееттолько тривиальное решение, если ранг матрицы системы (в данном случае 3) равен количеству переменных (в данном случае 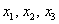– 3 шт.).

Разогреваемся и настраиваем свой радиоприёмник на волну элементарных преобразований:

Пример 2

Решить однородную систему линейных уравнений

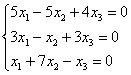
Из статьи Как найти ранг матрицы? вспоминаем рациональный приём попутного уменьшения чисел матрицы. В противном случае вам придётся разделывать крупную, а частенько и кусачую рыбу. Примерный образец оформления задания в конце урока.

Нули – это хорошо и удобно, однако на практике гораздо более распространен случай, когда строки матрицы системы линейно зависимы. И тогда неизбежно появление общего решения:

Пример 3

Решить однородную систему линейных уравнений

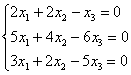
Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду. Первое действие направлено не только на получение единичного значения, но и на уменьшение чисел в первом столбце:

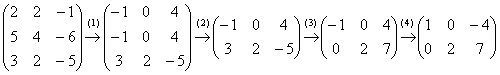
(1) К первой строке прибавили третью строку, умноженную на –1. Ко второй строке прибавили третью строку, умноженную на –2. Слева вверху я получил единицу с «минусом», что зачастую намного удобнее для дальнейших преобразований.

(2) Первые две строки одинаковы, одну из них удалили. Честное слово, не подгонял решение – так получилось. Если выполнять преобразования шаблонно, то линейная зависимость строк обнаружилась бы чуть позже.

(3) К третьей строке прибавили вторую строку, умноженную на 3.

(4) У первой строки сменили знак.

В результате элементарных преобразований получена эквивалентная система:

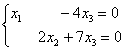
Алгоритм работает точно так же, как и для неоднородных систем. Переменные 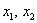, «сидящие на ступеньках» – главные, переменная 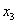, которой не досталось «ступеньки» – свободная.

Выразим базисные переменные через свободную переменную:

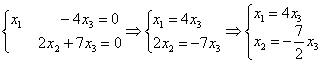
Ответ: общее решение: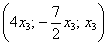

Тривиальное решение входит в общую формулу, и записывать его отдельно излишне.

Проверка выполняется тоже по обычной схеме: полученное общее решение необходимо подставить в левую часть каждого уравнения системы и получить законный ноль при всех подстановках.

На этом можно было бы тихо-мирно закончить, но решение однородной системы уравнений часто требуется представить в векторной форме с помощьюфундаментальной системы решений. Пожалуйста, временно забудьте обаналитической геометрии, поскольку сейчас речь пойдёт о векторах в общем алгебраическом смысле, который я немного приоткрыл в статье про ранг матрицы. Терминологии тушеваться не нужно, всё довольно просто: