Указания по выполнению работы №1

Рассмотрим построение годографа Михайлова по характеристическому полиному САУ:

(8.6)

Подставив в характеристический полином (8.6) вместо λ мнимую переменную jω, получим комплексную функцию

(8.7)

После возведения переменной jω в соответствующие степени выражение можно разбить на вещественную и мнимую части

(8.8)

где

(8.9)

Задаваясь дискретными значениями w от 0 до Ґ, можно вычислить соответствующие им значения U_D(w) и V_D(w) и по ним на комплексной плоскости построить годограф Михайлова (Рисунок 8.12).

В последнем квадранте годограф должен уйти в бесконечность. На рисунке 8.12(а) изображены годографы устойчивых, а на рисунке 8.12(б) – неустойчивых систем.

Рисунок 8.12 Годограф Михайлова

Пример 8.1 Определим устойчивость системы с помощью критерия Михайлова.

Уравнение непрерывной части системы описывается урав­нением (8.10).

Объект управления (ОУ) описывается линейным диффе­ренциальным уравнением третьего порядка:

(8.10)

Пусть Т₁ = 8, Т₂ = 12, Т₃ = 5, k = 3. Коэффициент Т_n = 0.175 в пер­вой контрольной работе не используется. Уравнение (1) примет вид:

(8.11)

Передаточная функция ОУ в общем случае может быть представлена в виде отношения

,

где и – изображения по Лапласу выходной и вход­ной переменных ОУ, соответствующих левой и правой частям уравнения 1. Отсюда, передаточная функция будет иметь вид:

, (8.12)

или

. (8.13)

Подставим iω в выражение (8.13) вместо p. Получим:

. (8.14)

Используем критерий устойчивости Михайлова для незамк­нутой системы. Этот критерий является графоаналитическим. Построим годограф Михайлова на основе полинома ПФ незамкнутой системы.

(8.15)

Рисунок 8.13 - Годограф Михайлова для незамкнутой системы

Порядок системы n = 3. Поэтому для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова, начина­ясь на действительной оси, проходил последовательно через три квадранта, уходя в бесконечность в n-том квадранте. Что и происходит в действительности.

По аналогии с незамкнутой системой применим критерий Михайлова к замкнутой системе.

Передаточная функция (ПФ) замкнутой системы по от­ношению к разомкнутой ПФ представляется выражением:

. (8.16)

Отсюда,

.

Подставим iω в выражение (6) вместо p. Получим:

. (8.17)

Используем критерий устойчивости Михайлова для замк­нутой системы. Этот критерий является графоаналитическим. Построим годограф Михайлова на основе полинома ПФ замкнутой системы.

.

По виду годографа определяем, что замкнутая система ус­тойчива, так как годограф последовательно проходит три квад­ранта.

Рисунок 8.14 - Годограф Михайлова для замкнутой системы

Пример 8.2 Расчет устойчивости систем. Рассчитать устойчивость системы, заданной следующей структурной схемой (рис 8.15.) и построить кривую Михайлова.

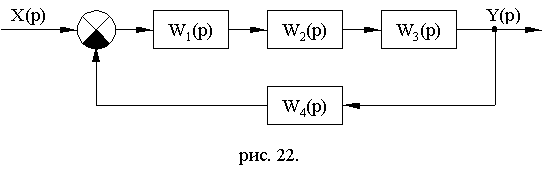
Рис. 8.15

W₁(P)=k₁; W₂(P)= 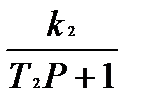;W₃(P)= 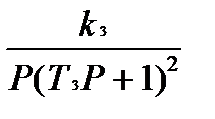; W₄(P)= .

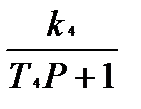Параметры звеньев: k₁=12; k₂=80; k₃=0.15; k₄=2; T₂=0.5; T₃=10; T₄=2.

Запишем эквивалентную передаточную функцию системы

W_зам(р) = .

Запишем передаточную функцию системы, разомкнутой по главной обратной связи.

W_раз(p) = W₁(P) ×W₂(P) ×W₃(P) ×W₄(P) = .

Характеристическое уравнение системы.

D(p)=1+ W_раз(p)=0 ® D(p)=1+ = 0;

K_э+(Т₂Т₃р³+Т₂р²+Т₄р+р)(Т₃²р²+2Т₃р+1)=0; Kэ=К₁К₂К₃К₄;

K_э + Т₂Т₄Т₃² р⁵ + (2Т₂Т₄Т₃ + Т₂Т₃² + Т₄Т₃²) р⁴ + (Т₄Т₂ + 2Т₂Т₃ + 2Т₄Т₃ + Т₃²) р³ +
(Т₂ + Т₄ + 2Т₃) р² + р = 0 ® .

Подставляя численные значения, получаем:

.

Критерий Михайлова.

Уравнение характеристического вектора получим из характеристического уравнения заменой оператора р®jw.

D(p)= 100р⁵+270р⁴+151 р³+ 22,5р²+ р+288=0;

D(jw)=100( jw)⁵+270 (jw)⁴+151( jw)³+22,5( jw)²+jw+288 = 100jw⁵+270jw⁴-151jw³- -22,5jw²+jw+288 = (288-22.5w²+270w⁴)+jw(1-151w²+100w⁴)=Re(w)+Im(w).

Изменяя w в интервале 0<w<¥, рассчитываем Re(w) и Im(w) и заносим в таблицу 1.

Таблица 1

w		0.1	0.5				¥
Re		287.9		535.5			¥
Im		-0.05	-15.3	-50			¥

Т.к. годограф начинается на положительном отрезке вещественной оси (рис. 8.16.), но не обходит 5 квадрантов, то система неустойчива.

Рис. 8.16

Пример 8.3 По критерию устойчивости Михайлова определить устойчивость САУ по заданному характеристическому полиному:

Годограф Михайлова построим примерно, определив координаты пересечения его с осями координат.

С учетом того, что годограф Михайлова строится при изменении w от 0 до +¥, определим положительные корни уравнения : и неотрицательные корни уравнения :

Координаты пересечения годографа Михайлова с осями координат (в порядке возрастания частоты):

1)

2)

3)

4)

5)

Примерный вид годографа Михайлова для полученных данных показан на рис.8.17. Исследуемая система устойчива.

Y

0 Х

Рис.8.17