Геометрический и физический смысл производной

Вертикальная

Вертикальная асимптота — прямая вида 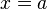при условии

существования предела .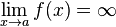

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

1.

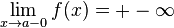
2.

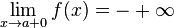
Замечание: обратите внимание на знаки бесконечностей в этих равенствах.

Горизонтальная

Горизонтальная асимптота — прямая вида 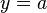при условии существования предела

.

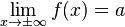Наклонная

Наклонная асимптота — прямая вида 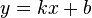при условии существования пределов

Пример наклонной асимптоты

1.

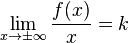
2.

Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.

Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен 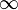), то наклонной асимптоты пр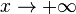и (или 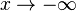) не существует.

Связь между наклонной и горизонтальной асимптотами

Если при вычислении предела 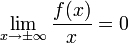, то наклонная асимптота совпадает с горизонтальной.

Горизонтальная асимптота является частным случаем наклонной при 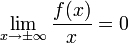, из этого следует что

1. Функция не может иметь наклонную асимптоту одновременно с горизонтальной при 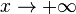, аналогично для 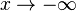, но так же возможен случай когда и вовсе нет асимптот.

2. Существование указанных в п. 1.) асимптот напрямую связано с существованием соответствующих пределов.

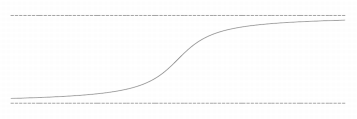
График функции с двумя горизонтальными асимптотами

Нахождение асимптот

Порядок нахождения асимптот

1. Нахождение вертикальных асимптот.

2. Нахождение двух пределов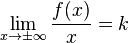

3. Нахождение двух пределов :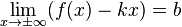

Если 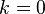в п. 2.), то 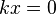, и предел 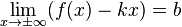находится по формуле горизонтальной асимптоты, .

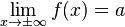Наклонная асимптота — выделение целой части

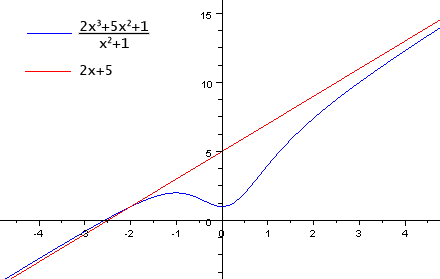
Также наклонную асимптоту можно найти, выделив целую часть. Например:

Дана функция .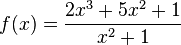

Разделив нацело числитель на знаменатель, получим:

.

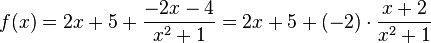При 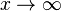, , 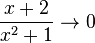то есть:

,

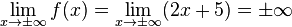и 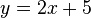является искомым уравнением асимптоты.

15 вопрос:

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной —интегрирование.

История

В классическом дифференциальном исчислении производная чаще всего определяется через понятия теории пределов, однако исторически теория пределов появилась позже дифференциального исчисления.

Русский термин «производная функции» впервые употребил В. И. Висковатов.^[1]

Определение

Пусть в некоторой окрестности точки 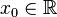определена функция 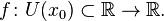Производной функции называется такое число 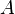, что функцию в окрестности 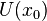можно представить в виде

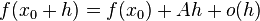
если 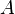существует.

Геометрический и физический смысл производной