Типы информации и доверительные интервалы

Ранее было отмечено, что энергетические системы (ЭС) и их объедине-ния относятся к классу больших систем (БС). Более того, на любой ступени иерархии они являются одними из наиболее ярко выраженных представителей больших систем технико-экономического типа. ЭС обладает всеми главными свойствами БС, которые существенны при выработке решений о их поведении.

Ознакомление с любой БС и дальнейшее принятие тех или иных реше-ний всегда начинаются с изучения имеющейся предварительной (априорной) информации о БС. Процесс принятия решений можно всегда истолко­вать как процесс преобразования информации. Под информацией понимают получен-ные для тех или иных целей сведения о каком-либо событии (или объекте изу-чения). Использование информации обогащает наши знания об этом событии, уменьшает неопределенность этих знаний. Кроме понятия «информация» пользуются ещё и другими терминами - «сведения» или «данные». Сведения – это полученные сообщения, для которых отсутствует какая-либо оценка их

полезности для лица, получив­шего эти сообщения. Поэтому иногда можно встретить упрощенное понятие информации, как полезные сведения.

Информация всегда как-то отражает свойства тех или иных событий. В практических задачах различают полную и неполную информации. Первая описывает события достаточно полно в смысле удовлетворения требованиям данной задачи. Ее использование практически полностью снимает неопре-деленность представления о событии. Поэтому часто ее называют определен-ной. Со­ответственно неполная информация сохраняет некоторую частичную неопределенность представления о событии. Поэтому ее можно назвать еще и частично неопределен­ной. Во многих работах довольно часто встречается тер­мин «неопределенная информация», который надо понимать как синоним частично неопределенной информации. Строго говоря, неопределенные сооб-щения не являются информацией, поскольку они не отражают свойства собы­тия и поэтому не могут быть использованы в целях обобщения наших знаний о событии.

Все события можно разделить на два класса – детерминированные и слу-чайные. Поэтому информацию о детер­минированных событиях называют детерминированной, а о случайных – вероятностной. Таким образом, следует различать четыре группы информации: детерминирован­ная полная, детерми-нированная – частично неопределенная, вероятностная полная и вероятност-ная частично неопределенная. Здесь вероятностная полная понимается в ста-тистическом смысле: эта информация достаточна, чтобы получить вероятност-ные характеристики о том или ином событии при наличии допустимых для данной задачи доверительных интервалов.

Обращаясь к частично неопределенной информации, можно заметить одну общую черту для обеих ее разно­видностей. Частичная неопределенность означает, что эта информация ставит в соответствие данному состоянию собы-тия не точку, а некоторую область определения в пространстве состояний. Внутри этой области состояние не определено ни как детерминированное, ни как вероятностное. Более того, границы областей оказываются «размытыми или расплывчатыми», их не удается четко зафиксировать. В результате о сос-тоянии события можно судить лишь с большей или меньшей погрешностью, определяемой этими, расплывчатыми границами области определения состо-яния. На рис.1.1 представлена область прогноза нагрузки энергосистемы Р(t) Между границами этой области для каждого t нельзя отдать предпочтение ни одному из значений Р ни в детерминированном, ни в вероятностном смысле. Именно эта область и определяет частичную неопределённость сведений о Р(t).

Важным методическим следствием является то обстоятельство, что ис-пользование частично неопределенной информации оказывается одинаковым, вне зависимости от принадлежности события к детерминированным или слу-чайным. Поэтому можно упростить терминологию, объединить обе группы в одну и назвать ее для обоих случаев частично неопределенной или даже нео-пределенной (если есть уверенность, что этот последний термин не может

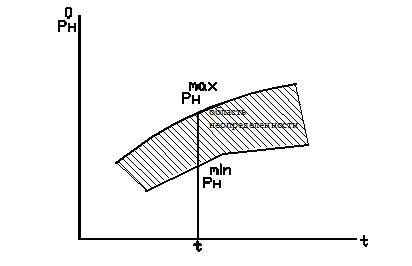
Рис. 1.1. Область неопределённости

привести к недоразумениям). Но тогда и две другие группы информации мож-но назвать проще – детерминированная и вероятностная, опустив за ненадоб-ностью термин «полная» или «определенная».

Применительно к прогнозу Р(t) детерминированная информация пред-ставляется единственной кривой P(t), а вероятностная – вероятностными характеристиками P(t) для всех t. Для неопределенной информации весь спектр P(t) в пределах зоны неопределенности не имеет ни вероятностных, ни детерминированных характеристик.

Наконец, существуют единичные, уникальные собы­тия, встречающиеся так редко, что объективно невозмож­но поставить им в соответствие какие-либо вероятности их появления. Тогда в одних случаях их относят к неопре-деленным, а в других, на основе общих соображе­ний, глубины понимания системы и решаемой задачи, ин­туиции и личных вкусов исследователь может приписать им «субъективную» вероятность, если это кажется необходимым.

Неопределенность информации не означает принципиальную невозмо-жность познания события, которое она отражает. Неопределенность есть след-ствие двух обстоятельств: неполноты полученных сведений и ошибок при формировании, передаче, приеме и обработке информации. Источниками оши-бок информации для технико-экономических систем являются: объект и сред-ства наблюдения, передачи и обработки данных, внешняя среда и, наконец, сам исследователь («индивид»). Эти источники объективно существуют, но их влияние может быть уменьшено по мере совершенствования мер борьбы с ними.

Неопределенность и неточность информации часто уменьшается в про-цессе реализации решения, принятого на её основе. Дело в том, что процесс реализации может сопровождаться получением дополнительной информации за счет обратных связей от управляемой системы к системе управления. Это может служить источником вне­сения корректив в решение, т. е. использования адаптации к изменяющейся информации и изменяющимся рассматриваемым явлениям.

Особо следует остановиться на том типе неточности, который обычно называют расплывчатостью. Расплывчатость является основным источником неточности не только информации, но и многих процессов принятия решений. Приведенная на рис.1.1 зона неопределенности нагрузки P(t) при расплывча-тых границах является одним из примеров расплывчатой информации. Однако расплывчатость относится не только к информации, но и ко многим другим понятиям, которые характеризуются нечетко выраженными общими свойст-вами или признаками. Например, само понятие «большая система» является расплывчатым, так как термин «большая» не определен точно по размерности, поскольку нет четких границ между «большой» и «небольшой» системами. Понятия «значительный экономический эффект», «практически экономичный режим» и многие другие – все это примеры расплывчатых понятий. Поскольку каждое из них является собирательным и относится не к одному, а к множест-ву явлений, объединенных общим расплывчатым признаком, то обычно при-меняют термин «расплывчатое множество». Кроме термина «расплывчатый» используют его равноправные заменители - «нечеткий», «размытый», «нечетко определенный».

Легко видеть, что в любой деятельности человека встречается очень много жизненных ситуаций, когда при­ходится сталкиваться с необходимостью принятия реше­ний в расплывчатых условиях, где даже цели решения, а также ограничения и последствия принятия тех или иных альтернативных действий точно не известны. Все эти ситуации можно разделить на два класса – веро-ятностные и размытые, причем разница между ними достаточно существенна. Задачи в расплывчатых условиях, особенно при несколько нечетких целях, не могут быть решены точно. В этих случаях говорят лишь о сужении множества альтернатив, подлежащих сравнению и выбору из них той, которая считается лучшей с точки зрения лица, принимающего решение. Однако на практике часто общие задачи в расплывчатых условиях стремятся заменить частными задачами в более определенных условиях. При этом, если возможно, то игно-рируется факт расплывчатости.