Векторная интерпретация задачи
Большинство детерминированных задач прикладной области вычислительных систем сетей, являются линейными, поэтому векторная интерпретация задач здесь имеет достаточно большую общность. В частности, всегда, когда может быть определено некое желаемое или оптимальное решение, могут быть определены исходные способы решения, при необходимости задана область оптимальных решений, применим данный подход. Рассмотрим его применительно к задачам синтеза расписаний реального времени.
Рассматриваемая детерминированная задача теории расписаний состоит в определении очередности передачи прав на занятие ресурса, минимизирующей его производительность при выполнении ограничений реального времени. Более подробно постановку задачи синтеза расписаний реального времени мы рассмотрим на практических занятиях, здесь лишь отметим, что ограничения реального времени 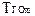 на время решения различных задач (задача должна быть гарантированно решена за этот промежуток времени) в одной системе реального времени могут сильно различаться, ввиду их разнородности (например, при построении системы управления с соответствующими различными заданными периодами может потребоваться измерять скорость, температуру, плотность чего-либо и т.д. и т.п.). В этом случае использование бесприоритетного режима обслуживания в реальном времени (по очереди) может оказаться неоптимальным, требующим большого увеличения производительности общего ресурса. Требуется построить оптимальную для конкретного приложения приоритетную дисциплину обслуживания реального времени.
на время решения различных задач (задача должна быть гарантированно решена за этот промежуток времени) в одной системе реального времени могут сильно различаться, ввиду их разнородности (например, при построении системы управления с соответствующими различными заданными периодами может потребоваться измерять скорость, температуру, плотность чего-либо и т.д. и т.п.). В этом случае использование бесприоритетного режима обслуживания в реальном времени (по очереди) может оказаться неоптимальным, требующим большого увеличения производительности общего ресурса. Требуется построить оптимальную для конкретного приложения приоритетную дисциплину обслуживания реального времени.
Рассмотрим интерпретацию постановки задачи на рисунке.
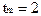
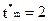
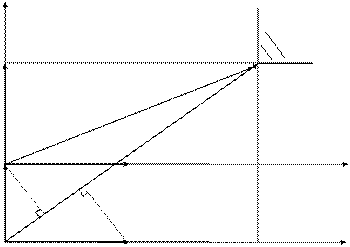
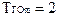
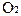
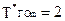
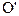
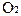
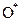
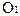
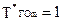
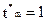
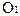
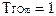
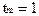
По осям координат откладываются временные характеристики решения задачи m-го типа (в частности, 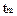 ) и ограничения реального времени
) и ограничения реального времени 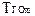 , которые ограничивают некоторую допустимую область решений (однако, в отличие от предшествующего случая (задача линейного программирования), допустимая область решений здесь уже иная, задается условиями
, которые ограничивают некоторую допустимую область решений (однако, в отличие от предшествующего случая (задача линейного программирования), допустимая область решений здесь уже иная, задается условиями 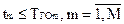 ). Особенностью является и то, что исходно задано M способов решения задачи, при каждом весь квант времени (с учетом затрат времени на выбор заявки из очереди) предоставляется заявке одной из M очередей. Соответственно имеем M векторов равной длины, совпадающих по направлению с осями системы координат - векторы
). Особенностью является и то, что исходно задано M способов решения задачи, при каждом весь квант времени (с учетом затрат времени на выбор заявки из очереди) предоставляется заявке одной из M очередей. Соответственно имеем M векторов равной длины, совпадающих по направлению с осями системы координат - векторы  и
и 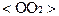 (см. рис.). В этом случае уже имеет смысл говорить не о максимальной длине проекции на идеальный вектор
(см. рис.). В этом случае уже имеет смысл говорить не о максимальной длине проекции на идеальный вектор 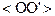 , а о минимальной, что реализуется при откладывании векторов по осям координат, так как целесообразно обслужить максимальное число заявок за ограниченное время, или о достижимости ограничений
, а о минимальной, что реализуется при откладывании векторов по осям координат, так как целесообразно обслужить максимальное число заявок за ограниченное время, или о достижимости ограничений 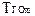 по M осям.
по M осям.
Естественно, что при синтезе расписания, первую очередь, имеет смысл откладывать вектор в том m-м направлении, которое может быть получено из условия 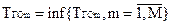 , т.е. выбираем самое «жесткое» ограничение, которое должно быть выполнено за минимальное время. На рис. это ограничение
, т.е. выбираем самое «жесткое» ограничение, которое должно быть выполнено за минимальное время. На рис. это ограничение 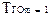 . Предоставим ресурс выбранной заявке на фиксированное время занятия, задаваемое продолжительностью временного кванта, что на рис. соответствует отложению вектора
. Предоставим ресурс выбранной заявке на фиксированное время занятия, задаваемое продолжительностью временного кванта, что на рис. соответствует отложению вектора  . Далее требуется сформировать новую систему координат. Особенностью ее получения будет перенос системы координат в направлении и на величину векторов
. Далее требуется сформировать новую систему координат. Особенностью ее получения будет перенос системы координат в направлении и на величину векторов 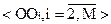 , что на рис. соответствует переносу на вектор
, что на рис. соответствует переносу на вектор 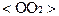 .
.
Поясним физический смысл получения новой системы координат. После обслуживания заявки m=1 ее место занимает следующая заявка из этой очереди, для которой ограничение на время обслуживания совпадает с исходным. Ни одна из заявок других очередей за это время не обслуживается или после окончания кванта ограничение на время обслуживания этих заявок уменьшится ровно на продолжительность кванта. Многоэтапная процедура оптимизации выполняется до тех пор, пока заявки всех очередей не будут обслужены за ограниченное время, и результатом решения задачи будет оптимальное расписание обслуживания при заданной длине кванта, которая, собственно, и задает производительность ресурса. Если заявки всех очередей невозможно обслужить с учетом заданных временных ограничений, необходимо повышать производительность ресурса, что приведет к уменьшению длины кванта, задающего продолжительность обслуживания одной заявки. Затем процедура синтеза расписания должна быть выполнена вновь. Если заявки всех очередей можно обслужить за время, меньшее задаваемого ограничениями, можно увеличить продолжительность кванта с повторным выполнением процедуры для оптимизации производительности ресурса.
Утверждение. Продолжительность временного кванта обслуживания заявки в системе 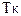 задается условием
задается условием 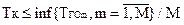 .
.
Доказательство. Чтобы иметь возможность обслужить M заявок с совпадающими 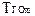 (худший для системы случай - бесприоритетная дисциплина обслуживания), необходимо и достаточно, чтобы за время
(худший для системы случай - бесприоритетная дисциплина обслуживания), необходимо и достаточно, чтобы за время 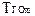 каждая заявка единожды получила доступ к ресурсу, что возможно при условии выбора продолжительности кванта, равной
каждая заявка единожды получила доступ к ресурсу, что возможно при условии выбора продолжительности кванта, равной 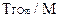 .
.
Таким образом, использование векторного метода синтеза расписаний состоит в следующем - выбирая очередность представленного кванта - синтезируем дисциплину обслуживания; выбирая же величину кванта – определяем оптимальную производительность ресурса.
