Пример решения задачи ЛП симплекс-методом

Задача. Для реализации трёх групп товаров коммерческое предприятие располагает тремя видами ограниченных материально-денежных ресурсов в количестве 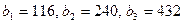единиц. При этом для продажи 1 группы товаров на 1 тыс. руб. товарооборота расходуется ресурса первого вида в количестве a₁₁=4 единиц, ресурса второго вида в количестве a₂₁=3 единиц, ресурса третьего вида в количестве a₃₁=12 единиц. Для продажи 2 и 3 групп товаров на 1 тыс. руб. товарооборота расходуется соответственно ресурса первого вида в количестве a₁₂=8, a₁₃=2 единиц, ресурсов второго вида в количестве a₂₂=8, a₂₃=4 единиц, ресурсов третьего вида в количестве a₃₂=4, a₃₃=6 единиц. Прибыль от продажи трёх групп товаров на 1 тыс. руб. товарооборота составляет соответственно c₁=8, c₂=6, c₃=6(тыс. руб.). Определить плановый объём и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной. Сведём условие задачи в таблицу.

Табл.9

Виды ресурсов	Норма затрат ресурсов	Объём ресурсов bi
I гр.	II гр.	III гр.
Прибыль				-

Запишем математическую модель задачи:

При ограничениях

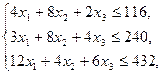
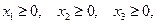найти такой план 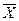, что

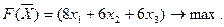
Для получения первого опорного плана 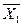преобразуем систему ограничений к системе уравнений:

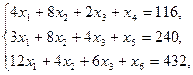
Целевая функция для 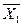примет вид:

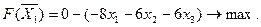
При этом условии построим первый опорный план, расположив его в первой симплексной таблице. Учитывая шаги 1-5, улучшаем план, получаем вторую и третью симплексные таблицы.

Табл.10

План	БП	Ресурсы плана	Коэффициенты при переменных
x1	x2	x3	x4	x5	x6
I	x4
x5
x6
Индексная строка		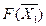	-8	-6	-6				-

Табл.11

План	БП	Ресурсы плана	Коэффициенты при переменных
x1	x2	x3	x4	x5	x6
II	x1				0.5	0.25
x5				2.5	-0.75			61.2
x6			-20		-3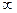
Индексная строка		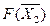			-2				-

Табл.12

План	БП	Ресурсы плана	Коэффициенты при переменных
x1	x2	x3	x4	x5	x6
III	x3					0.5
x5		-5	-8		-2
x6			-20		-3
Индексная строка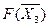

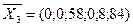
тыс.руб.

На 3 итерации получился план III, который можно считать оптимальным, и.к. все коэффициенты индексной строки неотрицательны. Следовательно, необходимо продавать товаров III группы 58 единиц, при этом коммерческое предприятие получает максимальную прибыль 348 тыс. руб. Товары I и II групп не реализуются, т.к. x₁=0, x₂=0.

В оптимальном плане среди базисных переменных находятся дополнительные переменные x₅ и x₆. Это указывает на то, что ресурсы второго и третьего вида, недоиспользованы соответственно на 8 и 84 единицы, а ресурс I вида использован полностью, т. е. x₄=0.

В индексной строке III плана в столбцах переменных x₁, x₂, x₄, не вошедших в состав базисных, получены ненулевые элементы, поэтому оптимальный план задачи ЛП является единственным.