Выпуклость и вогнутость графика функции
Это свойство кривой мы часто используем в реальной действительности. Математически его можно описать по-разному.
 Рис. 8.12. График функции Рис. 8.12. График функции  , являющийся выпуклым на данном участке. , являющийся выпуклым на данном участке. |
Будем называть график функции  ВЫПУКЛым (рис. 8.12) (ВОГНУТым (рис. 8.13)) на участке, соответствующем изменению x от a до b, если точки любой дуги
ВЫПУКЛым (рис. 8.12) (ВОГНУТым (рис. 8.13)) на участке, соответствующем изменению x от a до b, если точки любой дуги  графика функции
графика функции  , где
, где  и
и  , лежат выше (ниже) хорды, стягивающей эту дугу.
, лежат выше (ниже) хорды, стягивающей эту дугу.
 Рис. 8.13. График функции Рис. 8.13. График функции  , являющийся вогнутым на данном участке. , являющийся вогнутым на данном участке. |
Важно отметить, что любая дуга графика функций с концами, имеющими абсциссы x1 и x2  , должна обладать указанным свойством. Если это условие не выполнено, то расположение графика функции выше (ниже) только одной хорды, имеющей абсциссы a и b, не гарантирует выпуклости (вогнутости) графика функции
, должна обладать указанным свойством. Если это условие не выполнено, то расположение графика функции выше (ниже) только одной хорды, имеющей абсциссы a и b, не гарантирует выпуклости (вогнутости) графика функции  на отрезке
на отрезке  (рис. 8.14 и рис. 8.15).
(рис. 8.14 и рис. 8.15).
 Рис. 8.14. График функции, не являющийся выпуклым на отрезке Рис. 8.14. График функции, не являющийся выпуклым на отрезке  . . |
В дальнейшем мы рассмотрим и другой способ введения этих понятий.
 Рис. 8.15. График функции, не являющийся вогнутым на отрезке Рис. 8.15. График функции, не являющийся вогнутым на отрезке  . . |
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ .
Построение графика функции часто значительно облегчается, если известны связанные с ним прямые, называемые асимптотами. Асимптоты вводятся для кривых, ветви которых уходят в бесконечность. Это может иметь место в случаях, когда функции неограниченны или заданы на неограниченном промежутке. Понятие асимптоты мы также введем не вполне строго, но в дальнейшем уточним.
Будем называть некоторую прямую
Y = ax + b
 а)б) Рис. 8.16. Некоторые случаи расположения кривой а)б) Рис. 8.16. Некоторые случаи расположения кривой  относительно асимптоты: а) кривая не пересекает асимптоту; б) кривая пересекает асимптоту. относительно асимптоты: а) кривая не пересекает асимптоту; б) кривая пересекает асимптоту. |
НАКЛОННОЙ АСИМПТОТОЙ для графика функции  , если к ней приближаются сколь угодно близко точки кривой при удалении в бесконечность. Она может не пересекаться с асимптотой (рис. 8.16, а) или приближаться к ней, пересекая ее конечное или бесконечное число раз (рис. 8.16, б).
, если к ней приближаются сколь угодно близко точки кривой при удалении в бесконечность. Она может не пересекаться с асимптотой (рис. 8.16, а) или приближаться к ней, пересекая ее конечное или бесконечное число раз (рис. 8.16, б).
Частным случаем наклонной асимптоты является горизонтальная.
Существует и рассматривается ВЕРТИКАЛЬНАЯ АСИМПТОТА. Так называется прямая x = a, если при стремлении x к a функция неограниченно возрастает или неограниченно убывает. Можно привести в качестве примера известные функции  (рис. 8.17) и
(рис. 8.17) и  (рис. 8.18), которые имеют вертикальные асимптоты соответственно
(рис. 8.18), которые имеют вертикальные асимптоты соответственно
 Рис. 8.17. Графики функции Рис. 8.17. Графики функции  ,вертикальной асимптоты ,вертикальной асимптоты 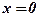 и горизонтальной асимптоты y = 0. и горизонтальной асимптоты y = 0. |
 Рис. 8.18. Графики функции Рис. 8.18. Графики функции  и вертикальных асимптот и вертикальных асимптот  . . |
 и
и 
Обратная функция
Пусть функция  задает взаимно однозначное соответствие между областью определения функции
задает взаимно однозначное соответствие между областью определения функции  и множеством ее значений
и множеством ее значений  , то есть каждый элемент
, то есть каждый элемент  из множества
из множества  является образом одного и только одного элемента
является образом одного и только одного элемента  из множества
из множества  . Так как при этом оказывается, что КАЖДОМУ элементу
. Так как при этом оказывается, что КАЖДОМУ элементу  ставится в соответствие ЕДИНСТВЕННЫЙ элемент
ставится в соответствие ЕДИНСТВЕННЫЙ элемент  , то можно говорить, что на множестве
, то можно говорить, что на множестве  определена функция, ОБРАТНАЯ ПО ОТНОШЕНИЮ К ДАННОЙ функции
определена функция, ОБРАТНАЯ ПО ОТНОШЕНИЮ К ДАННОЙ функции  , которую обозначают
, которую обозначают  ,
,

Если у обратной функции, как и у данной функции, аргумент обозначить за  , а зависимую переменную за
, а зависимую переменную за  , то обратная функция запишется в виде:
, то обратная функция запишется в виде:
 .
.
Наличие взаимно однозначного соответствия между множествами Х и Уобеспечивает существование обратной функции, чего нельзя добиться при других отображениях, которые можно установить между этими множествами.
Графики функций  и
и  , совпадают, а графики функций
, совпадают, а графики функций  и
и  тогда симметричны относительно прямой y = x, так как у них переставляются
тогда симметричны относительно прямой y = x, так как у них переставляются  и
и  .
.
Например, функция
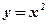 ,
, 
на отрезке, “области значений”, [-2; 0] имеет обратную функцию (риc. 8.19)
 ,
,  .
.
 Рис. 8.19. Взаимное расположение графиков прямой и обратной функций. Рис. 8.19. Взаимное расположение графиков прямой и обратной функций. |
Отметим, что функция  на промежутке [-2;2] уже не имеет обратной, так как, например, значению
на промежутке [-2;2] уже не имеет обратной, так как, например, значению  соответствует два значения
соответствует два значения  , что нарушает взаимную однозначность соответствия между множествами D( f )и E( f ).
, что нарушает взаимную однозначность соответствия между множествами D( f )и E( f ).
 Рис. 8.20. Обратная функция для немонотонной функции. Рис. 8.20. Обратная функция для немонотонной функции. |
Строгая монотонность функции является достаточным, но не необходимым условием существования ей обратной. Например, функция, которая изображена на рис. 8.20, не является строго монотонной, но она имеет обратную.
Сложная функция
Сложная функция не есть указание на трудности, связанные с ее исследованием. Это конкретное математическое понятие, основанное на идее отображения.
Пусть функция  отображает множество Xна множество Y, а функция
отображает множество Xна множество Y, а функция  отображает множество Yв множество Z. Тогда функция
отображает множество Yв множество Z. Тогда функция

называется СЛОЖНОЙ ФУНКЦИЕЙ, ИЛИ СУПЕРПОЗИЦИЕЙ (КОМПОЗИЦИЕЙ) ФУНКЦИЙ.
Она определена на множестве X и отображает его в множество Z.
При этом функция

называется ПРОМЕЖУТОЧНЫМ АРГУМЕНТОМ для функции
 .
.
Например, функция

может рассматриваться как сложная, образованная суперпозицией функций

и

Классификация функций
Выделим первоначально ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ :
–степенную: 
– показательную: 
– логарифмическую: 

– тригонометрические и обратные тригонометрические:


ЭЛЕМЕНТАРНЫМИ ФУНКЦИЯМИ будем называть совокупность всех функций, которые можно получить из основных элементарных функций путем применения к ним конечного числа арифметических операций (сложения, вычитания, умножения и деления), а также сложные функции, образуемые на их основе, как их композиция.
Во множестве элементарных функций выделяются следующие классы.
ЦЕЛЫМИ РАЦИОНАЛЬНЫМИ ФУНКЦИЯМИ называются многочлены с действительными коэффициентами

ДРОБНО-РАЦИОНАЛЬНЫМИ ФУНКЦИЯМИ называются функции, являющиеся отношениями многочленов:

Под РАЦИОНАЛЬНЫМИ ФУНКЦИЯМИ будем понимать совокупность целых рациональных и дробно–рациональных функций.
ИРРАЦИОНАЛЬНЫми ФУНКЦИямИ называются функции, образуемые применением к аргументу операций сложения, вычитания, умножения, деления и извлечения корня, а также сложные функции, образованные на их основе и не являющиеся рациональными.
Например, функция

иррациональна, так как является сложной, составленной из двух функций

 .
.
Функция  –дробно-рациональная, а функция
–дробно-рациональная, а функция  ,являющаяся степенной с дробным показателем 1/2 –иррациональная.
,являющаяся степенной с дробным показателем 1/2 –иррациональная.
АЛГЕБРАИЧЕСКИМИ ФУНКЦИЯМИназывается совокупность рациональных и иррациональных функций.
ТРАНСЦЕНДЕНТНЫМИ ФУНКЦИЯМИ – все элементарные функции, не являющиеся алгебраическими. В их числе основные элементарные функции, кроме степенных функций с рациональными показателями.
В математике кроме элементарных функций имеются и НЕЭЛЕМЕНТАРНЫЕ. К числу таких функций относится уже известная функция  ,
,  .
.
Неэлементарной является и функция Дирихле

Построение графика этой функции не представляется возможным, так как на любом сколь угодно малом отрезке из ее области определения найдутся как рациональные, так и иррациональные числа.
На рис. 8.21 приведена классификация элементарных функций.
Функция Дирихле лишний раз убеждает нас в том, что график не есть отличительный признак функциональной зависимости. Однако во многих случаях бывает полезно завершить исследование функций именно построением ее графика. Это требует не только знания свойств элементарных функций, но и владения простейшими приемами построения их графиков.
