Вычисление определителя матрицы

ВВЕДЕНИЕ

Методические указания представлены в виде набора практических и лабораторных работ для развития навыков моделирования и реализации решения инженерных задач. Задачи сопровождаются инструкциями выполнения. Предлагаемые упражнения и задания помогут усвоить технику использования MS Excel и найти эффективные способы решения практических задач.

ОСНОВНЫЕ ПОНЯТИЯ

Массивы

Массив данных – это совокупность однотипных элементов. Тип элементов в MS Excel определяется с помощью Формат Ячейки. В MS Excel можно работать с одномерными и двумерными массивами.

Одномерные массивы (векторы), состоят из элементов строк или столбцов, например, B2:B5, C9:G9 (рис. 1).

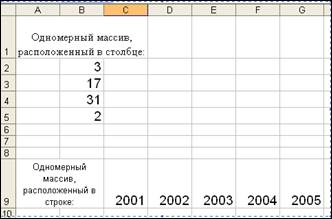
Рис. 1

Двумерные массивы (матрицы) состоят из элементов, располагающихся в прямоугольном диапазоне, например, A2:C3, B8:C12 (рис. 2).

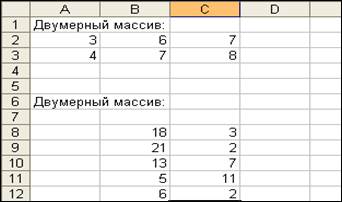
Рис. 2

Формулы массивов

Формулы массивов используются для того, чтобы производить вычисления над несколькими значениями (массивом значений), не производя копирования и заполнения.

Пример. Выполним сложение и вычитание двух векторов А=(а₁,а₂,...а_n) и B=(b₁,b₂,...b_n), где n = 4, например, (рис. 3).

Рис. 3

Инструкция для сложения элементов двух векторов (рис. 3):

1) Выделить диапазон (строка) D3:G3, где будет результат сложения;

2) Ввести знак равенства в строку формул;

3) Выделить первый массив D1:G1;

4) Вставить знак «плюс»;

5) Выделить второй массив D2:G2;

6) Нажать комбинацию клавиш Ctrl+Shift+Enter.

7) Просмотреть содержимое ячеек полученного вектора. В каждой ячейке будет отображена одна и та же формула

{=D1:G1+ D2:G2}.

Инструкция для вычитания элементов двух векторов (рис. 3):

1) Выделить диапазон (строка) D4:G4.

2) Ввести знак равенства.

3) Выделить первый массив D1:G1.

4) Вставить знак «минус».

5) Выделить второй массив D2:G2.

6) Нажать комбинацию клавиш Ctrl+Shift+Enter.

7) Просмотреть содержимое ячеек полученного вектора. В каждой ячейке будет отображена одна и та же формула

{=D1:G1- D2:G2}.

Изменить содержимое ячеек полученных строк (векторов) невозможно. Нельзя вставить столбец в вектор. При таких попытках будет выдано сообщение, что нельзя изменить часть массива.

Если при выполнении пункта 6 инструкций, нажать на клавиатуре клавишу Enter вместо клавиш Ctrl+Shift+Enter, то в этом случае формула вычислит только одно, первое значение вектора. Перейти в режим редактирования нужно нажатием клавиши F2. Затем одновременно нажать Ctrl+Shift+Enter.

Ошибки в формулах

При наборе формул могут быть допущены ошибки, например:

Набраны две арифметические операции подряд, пропущен оператор, например, (рис. 4 а) вод формулы =(A1+A2-/A4), при наборе допущена элементарная ошибка или пропущен адрес ячейки или ошибочно введены подряд две арифметические операции вычитания и деления (рис. 4 б–4 г).

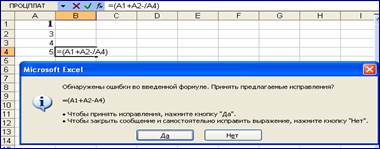
Рис. 4 а

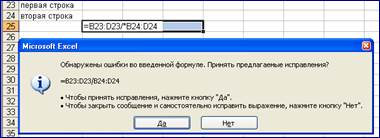
Рис. 4 б

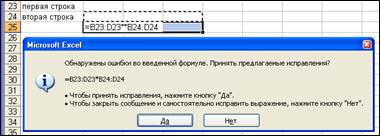
Рис. 4 в

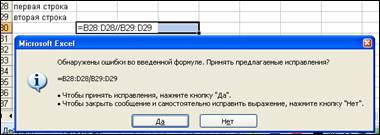
Рис. 4 г

Если при выполнении сложения элементов двух строк, ошибочно введены в формулу два знака арифметических операций подряд, сначала «+», а затем «–», то не будет ошибки, выполнится операция вычитания (рис. 5).

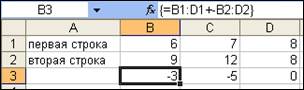
Рис. 5

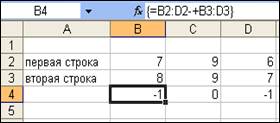
Рис. 6

Если при выполнении сложения элементов двух строк, ошибочно введены в формулу два знака арифметических операций подряд, сначала «–», а затем «+», то не будет ошибки, опять выполнится операция вычитания (рис. 6).

Пробел между вектором А1:D1 и В2:D2 означает пересечение диапазонов (рис. 7). Пересечения ячеек #ПУСТО!

Точка с запятой – это объединение диапазонов (рис. 8). В формуле ошибка.

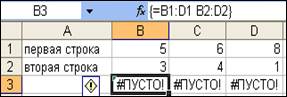
Рис. 7

Рис. 8

Могут возникать ошибки в формулах при попытках деления на 0

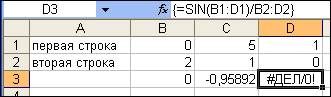
Рис. 9

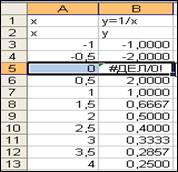
Рис. 10

Ошибки могут быть связаны с неопределенными именами ячеек, использованных в формулах: ошибка #ИМЯ? – не распознается имя, используемое в формуле (рис. 11–12). Имя адреса ячейки qod не было присвоено;

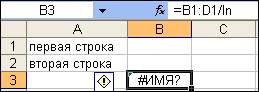
Рис. 11

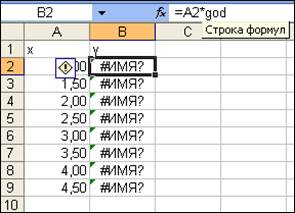
Рис. 12

Ошибка #ЗНАЧ! – используются операторы или аргументы недопустимого типа (рис. 13). В ячейке B12 возникла ошибка #ЗНАЧ! В этом случае это значит, что складываются содержимое ячеек А12 и А13 разного типа. A13 определено как тип дата, а A12 - как число.

Ошибка #Н/Д возникла в C6 неопределенных данных, т.е. не определены значения ячеек A6 и B6 (рис. 14).

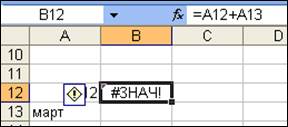
Рис.13

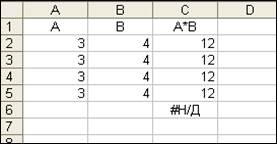
Рис. 14

В этом примере ошибка #ПУСТО! возникает при пересечении двух диапазонов, которые в действительности не имеют общих ячеек (рис. 15).

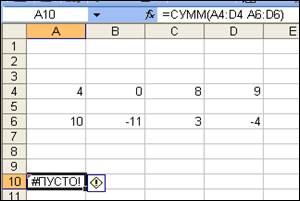
Рис. 15

Ошибка #ЧИСЛО! На рис. 16, 17 возникает при вычислении натурального логарифма от нуля, что невозможно.

Рис. 16

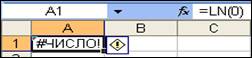
Рис. 17

Такого рода ошибка, как на рис. 18, происходит при «переполнении», когда числовое значение вычисляемой формулы слишком велико или слишком мало для используемого формата.

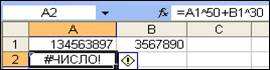
Рис. 18

Ошибка #ССЫЛКА! – неправильная ссылка на ячейку. В ячейке В8 (рис. 19) вычислена сумма элементов массива A1:B7. При попытке скопировать содержимое ячейки В8 в ячейку С1 и произошла ошибка. При копировании часто возникает ошибка #ССЫЛКА.

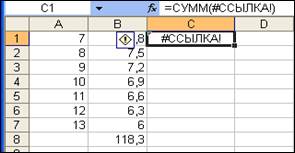
Рис.19

РАБОТА С МАТРИЦАМИ

Вычисление определителя матрицы

Процесс вычисления определителя матрицы (массива) даже выше третьего порядка трудоемок, но возможности MS Excel позволяют быстро и верно найти его. Например, чтобы вычислить определитель матрицы 4-го порядка, нужно:

1) ввести в ячейки листа MS Excel значения элементов матрицы по строкам, активизировать любую пустую ячейку, например С8, в которой будет получен результат вычисления определителя;

2) вызвать f_x (Функция…) меню Вставка (для MS Excel 2010 это меню Формула);

3) найти функцию МОПРЕД категории Математические (рис. 20);

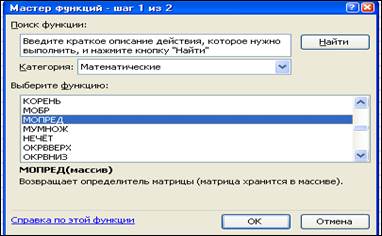
Рис. 20

4) откроется вспомогательное окно Аргументы функции (рис. 21);

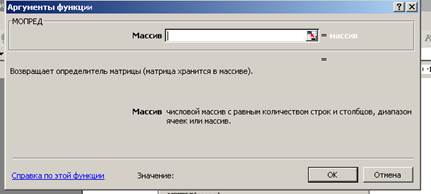
Рис. 21

5) В поле Массив помещаем адрес диапазона, в котором размещены элементы матрицы, например, B3:E6.

6) В указанной ранее ячейке, например С8, получим результат (рис. 22).

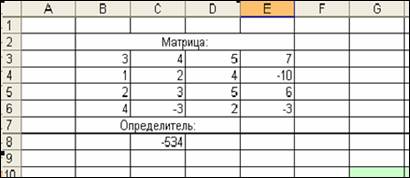
Рис. 22

Умножение матриц

При умножении двух матриц должна получиться матрица. Математический процесс нахождения произведения матриц трудоемок, сводится к вычислению сумм произведений по формуле. В MS Excel достаточно задать элементы матриц на листе по строкам, затем обратиться к функции МУМНОЖ Математической категории (рис. 23).

Получаем первый элемент произведения матриц. Он равен 6. Для получения всех элементов матрицу, выделяем место под матрицу-произведение нужной размерности, начиная с первого элемента, нажимаем клавишу F2 клавиатуры (рис. 24), затем Shft+Ctrl+Enter

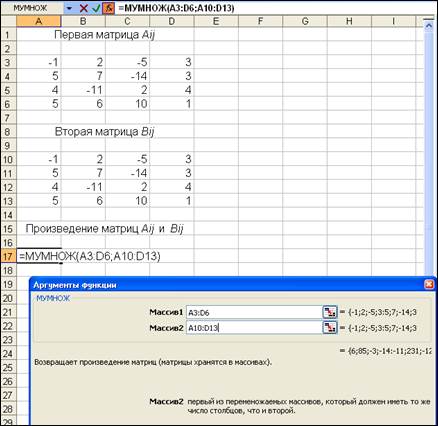
Рис. 23

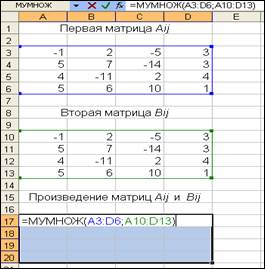
Рис. 24

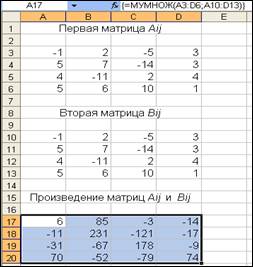
Рис. 25