Алгоритм метода Ньютона

1. Задать размерность задачи оптимизации п, коорди­наты начальной точки 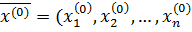, точ­ность поиска .

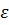2. Положить счетчик числа итераций .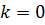

3. Определить направление вектора градиента целевой

функции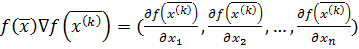

в точке 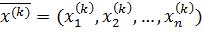. Для вычисления координат вектора градиента использовать разностную формулу (2.3) .

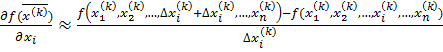4. Проверить условие окончания поиска

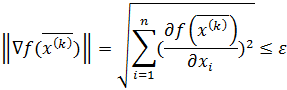
Если условие выполнено, то расчет окончен 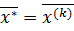, иначе перейти к пункту 5.

5. Сформировать матрицу Гессе 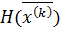, используя раз­ностные формулы вычисления вторых (2.5) и сме­шанных производных (2.6).

6. Проверить положительную определенность матрицы

Гессе 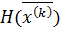. Если матрица положительно опреде­лена 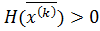, то перейти к пункту 7, иначе — к пункту 8.

7. Определить координаты точки 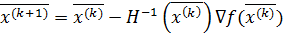и перейти к пункту 10.

8. Вычислить шаг 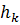по формуле (2.4), используя резуль­

таты вычислений пункта 3 и разностные формулы (2.5), (2.6).

9. Определить координаты точки 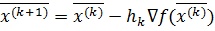по методу наискорейшего градиентного спуска.

10. Положить 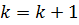и перейти к пункту 3.

Программы оптимизации

Для подтверждения работоспособности программы минимизации функции, из учебника [6], решим пример № 2.22. В данном примере, необходимо найти минимум целевой функции, методом Ньютона, с точностью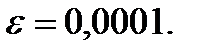

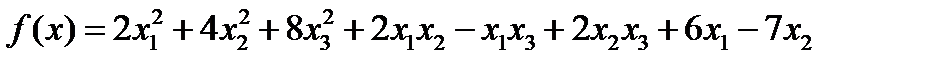
Для разработки программы была использована среда PascalABC.

Текст программы

Programlol;

labelstop;

constdx=0.0001;

typearray2D=array[1..4,1..4] ofreal;

varx,df:array ofreal;

d2f:array2D;

eps,h,grad,s:real;

i,j,n,q:integer;

functionf(x:array ofreal):real;

Begin

f:=2*sqr(x[1])+4*sqr(x[2])+8*sqr(x[3])+2*x[1]*x[2]-x[1]*x[3]+2*x[2]*x[3]+6*x[1]-7*x[3]

End;

Procedureinvert(n,q:integer;matr1:array2D;varmatr:array2D);

labelM1,M2;

vara:array[1..4,1..8] ofreal;

i,j,k,m:integer;

t:real;

Begin

m:=2*n; q:=0;

fori:=1 ton do

forj:=1 tom do

ifj<=n thena[i,j]:=matr1[i,j] else

ifj=n+i thena[i,j]:=1.0 elsea[i,j]:=0;

fori:=1 ton do

begink:=i;

M1:ifa[k,i]=0 then

beginq:=1;

ifk<n thenk:=k+1 else gotoM2;

gotoM1;

end;

ifq=1 then

forj:=1 tom do

begint:=a[k,j]; a[k,j]:=a[i,j]; a[i,j]:=t

end;

forj:=m downtoi doa[i,j]:=a[i,j]/a[i,i];

fork:=1 ton do

ifk<>i then

forj:=m downto1 do

a[k,j]:=a[k,j]-a[i,j]*a[k,i];

end;

q:=0;

fori:=1 ton do

forj:=1 ton domatr[i,j]:=a[i,j+n];

M2: end;

{Процедура вычисления координат вектора градиента и фомирования матрицы вторых производных}

procedureFor_Mat_d2f(n:integer; vargrad:real);

Var

i,j:integer;

s,f0:real;

Begin

//расчет производных

f0:=f(x);s:=0;

fori:=1 ton do

Begin

x[i]:=x[i]+dx;

df[i]:=(f(x)-f0)/dx;

s:=sqr(df[i]);

x[i]:=x[i]-dx;

end;

grad:=sqrt(s);

//расчет вторых производных

fori:=1 ton do

Begin

s:=-2*f(x);

x[i]:=x[i]+dx;

s:=s+f(x);

x[i]:=x[i]-2*dx;

s:=s+f(x);

x[i]:=x[i]+dx;

d2f[i,i]:=s/sqr(dx);

end;

//расчет смешанных производных

fori:=1 ton-1 do

forj:=i+1 ton do

Begin

s:=f(x); {1}

x[i]:=x[i]-dx; x[j]:=x[j]-dx;

s:=s+f(x); {4}

x[j]:=x[j]+dx;

s:=s-f(x);{2}

x[i]:=x[i]+dx; x[j]:=x[j]-dx;

s:=s-f(x);{3}

x[j]:=x[j]+dx;

d2f[i,j]:=s/sqr(dx);

d2f[j,i]:=d2f[i,j];

end;

end; {For_Mat_d2f}

//*****************

Begin

writeln('исходныеданные');

writeln;

write('введите размерность задачи оптимизации n=');

readln(n);

SetLength(x,n+1);

SetLength(df,n+1);

write('введите точность вычислений eps=');

readln(eps);

writeln('введите начальные значения переменных');

fori:=1 ton do

Begin

write('x[',i,']=');

readln(x[i]);

end;

Repeat

For_Mat_d2f(n,grad);

invert(n,q,d2f,d2f);

ifq=1 then beginwriteln('определительравеннулю');

gotostop end;

fori:=1 ton do

Begin

s:=0;

forj:=1 ton do

s:=s+d2f[i,j]*df[j];

x[i]:=x[i]-s;

end;

untilgrad<eps;

writeln;

writeln('результатыоптимизации:'); writeln;

fori:=1 ton do

writeln('x[',i,']=',x[i]);

writeln;

writeln('значение функции цели = ',f(x));

stop:readln;

end.

Результаты расчета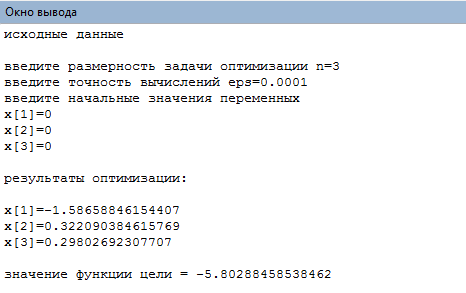

Полученные значения совпадают с результатами минимизации из учебника [6].