Постановка и геометрическая интерпретация

Многие задачи линейного программирования, возникающие в экономике и производстве, требуют решений, у которых компоненты целочисленны, то есть x_jÎZ, j=1, 2, …, n. Например, когда количество выпускаемой продукции измеряется в целых величинах, скажем, поштучно. Так, количество выпускаемых автомобилей, станков не может быть дробным. Раздел линейного программирования, изучающий методы решения таких задач, называется целочисленным линейным программированием, а задачи с таким условием - задачами целочисленного линейного программирования. В математической модели таких задач появляется дополнительное условие: x_jÎZ, j=1, 2, …, n:

c₁x₁+c₂x₂+…+c_nx_n®max(min)

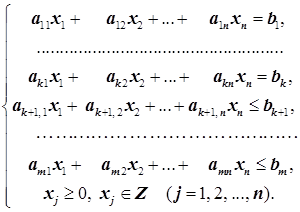(7.1)

В случае, когда задача имеет только две переменные:

c₁x₁+c₂x₂ ® max(min)

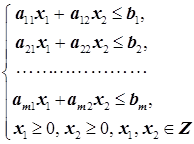(7.2)

она имеет простую геометрическую интерпретацию: решением задачи является точка в многоугольнике решений системы ограничений

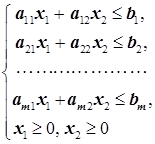(7.3)

с целочисленными координатами, в которой достигается экстремум целевой функции задачи. Такие задачи геометрически решаются по следующей схеме:

1. Построить многоугольник решений системы (7.1).

2. В многоугольнике решений, полученном в п.1, отметить точки с целочисленными координатами. Получается область допустимых решений (ОДР) задачи (7.2).

3. Построить линии уровня c₁x₁+c₂x₂=a целевой функции задачи.

4. В ОДР задачи (7.2), полученной в п.2, выбрать точку, в которой достигается требуемый экстремум.

5. Вычислить значение функции в найденной точке экстремума.

Пример 1. Решить задачу целочисленного программирования геометрическим способом:

2x₁+4x₂ ® max(min)

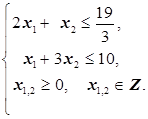
Решение. Действуем по вышеприведённой схеме:

1. Строим многоугольник решений системы (подробности опускаем) (Рис.4)

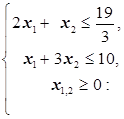
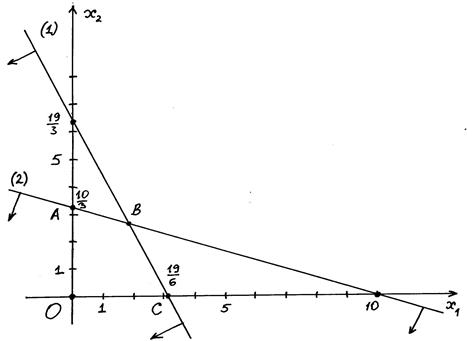
Рис.4

2. В многоугольнике решений, полученном в п.1, отмечаем точки с целочисленными координатами. Это точки (0, 0), (1, 0), (2, 0), (3, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2), (0, 3), (1, 3). Таким образом, ОДР задачи - это множество {(0, 0), (1, 0), (2, 0), (3, 0), (0, 1), (1, 1), (2, 1), (0, 2), (1, 2), (2, 2), (0, 3), (1, 3)} (Рис.5):

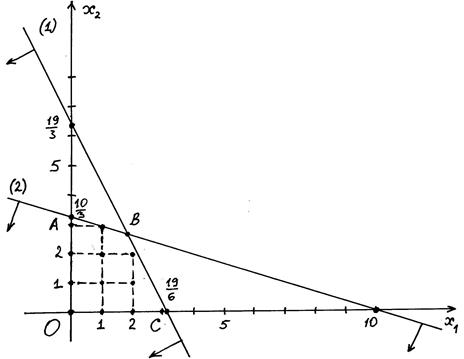
Рис.6

3. Cтроим линии уровня 2x₁+4x₂=a целевой функции задачи, ориентируясь на вектор 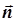=(1, 2) нормали этих линий, коллинеарный вектору 2 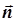=(2, 4) (Рис.7):

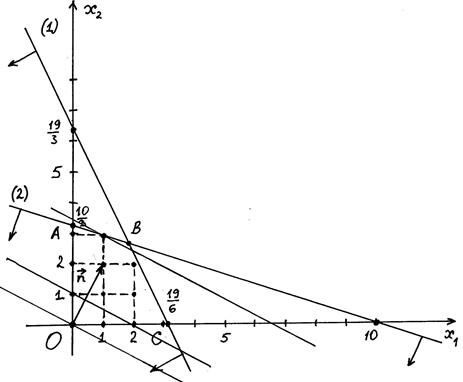
Рис.7

4. В ОДР задачи, полученной в п.2, выбираем точки, в которых достигаются требуемые экстремумы. Это точки (1, 3) - точка максимума, и (0, 0) - точка минимума.

5. Вычислим значение функции в найденных точках экстремума:

F_{max цел.}=F(1, 3)=2×1+4×3=14, F_{min цел.}=F(0, 0)=2×0+4×0=0.

Ответ: X_{max цел.}=(1, 3), F_{max цел.}=14; X_{min цел.}=(0, 0), F_{min цел.}=0.

Метод Гомори

Ясно, что когда задача целочисленного программирования имеет более двух переменных, её необходимо решать аналитическими методами. Одним из таких методов является метод Гомори. Он заключается в следующем.

1. Задача решается как обычная (симплекс-методом или методом искусственного базиса). Если в результате получилось целочисленное решение, то задача решена. В противном случае идём к шагу 1.

2. Допустим, b_i - нецелочисленная компонента решения, полученного на 1-м шаге, 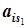, , 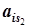…, 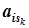- коэффициенты при свободных переменных 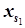, , 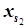…, 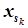соответствующего ограничения, из которых хотя бы один – не целый. Тогда к ограничениям, полученным в последней симплекс-таблице, добавляется дополнительное ограничение { 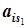} 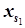+{ 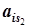} 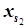+…+{ 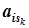} 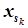³{b_i}, которое после введения очередной дополнительной переменной примет вид

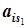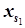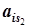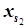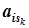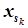{ } +{ } +…+{ } -x_n+1={b_i}. (1.1)

Здесь {a} - дробная часть числа a, n - количество переменных задачи в последней симплекс-таблице. Идём к пункту 1.

Если нецелочисленных компонент в оптимальном решении, полученном на первом шаге, несколько, то берём ту, у которой дробная часть наибольшая.

Если b_i - дробное, а все коэффициенты 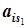, , 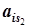…, 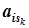при свободных переменных (в последней симплекс-таблице)являются целыми, то задача целочисленного программирования не имеет решения. Ясно, что задача целочисленного программирования решения не будет иметь, если задача решений не имеет вообще.

Пример 2. Решить задачу целочисленного программирования методом Гомори:

2x₁+4x₂®max

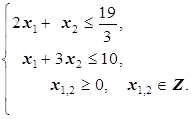
Решение. Решая первоначальную задачу, как обычную, получим следующие симплекс-таблицы:

Базис	Сб	Св. чл.					q1	q2
x1	x2	x3	x4
x3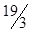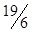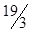
x4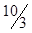
Dj		-2	-4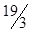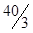
x3						-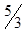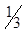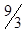
x2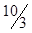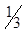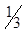
Dj		-				-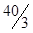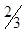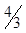
x1						-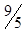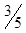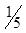
x2					-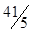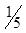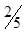
Dj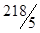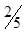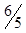

Таким образом, X₀= 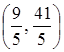- оптимальное решение, то есть нецелочисленных компонент в оптимальном решении, полученном на первом шаге, два. Найдём их дробные части и сравним:

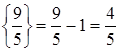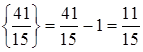, и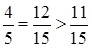

Поэтому составляем дополнительное ограничение по первой компоненте оптимального решения, которой в последней симплекс-таблице соответствует ограничение 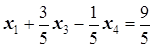. Имеем

, .

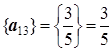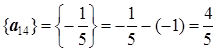Поэтому дополнительное ограничение (1.1) в нашем случае принимает вид

.

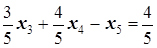Полученную задачу снова решаем как обычную:

Базис	Сб	Св. чл.						q3
x1	x2	x3	x4	x5
x1						-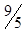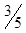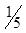
x2					-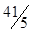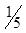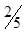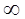
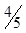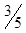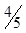-	-						-1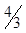
x1						-1
x2							-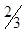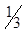
x3							-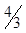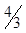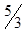
Dj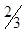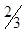

Получили оптимальное решение X₀= 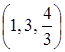данной задачи. Но так как исходная задача зависит только от двух переменных x₁ и x₂, которые принимают в этом решении целочисленные значения, то задача целочисленного программирования решена.

Ответ: X_цел.=(1, 3), F_{max цел.}=14.

Метод Гомори - не единственный аналитический метод решения целочисленной задачи. Разработан целый ряд аналитических методов, отличных от данного. В учебной литературе можно найти, например, метод ветвей и границ.

Транспортная задача