Метод простой итерации (Метод Якоби)
Пусть требуется решить систему
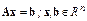 .
.
Представим 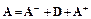 , где D – диагональная матрица с диагональными членами матрицы A;
, где D – диагональная матрица с диагональными членами матрицы A; 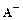 – часть матрицы A, лежащая ниже центральной диагонали,
– часть матрицы A, лежащая ниже центральной диагонали, 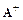 – часть матрицы A, лежащая выше центральной диагонали. Тогда
– часть матрицы A, лежащая выше центральной диагонали. Тогда
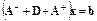 ,
,
или
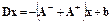 .
.
Запишем итерационный метод
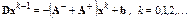
Разрешим его относительно 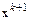 :
:
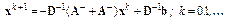
Эта форма удобна для реализации метода Якоби. Здесь итерационная матрица
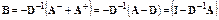 .
.
Матрица расщепления 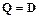 . Следовательно, при построении метода Якоби в качестве матрицы ращепления используется диагональ матрицы СЛАУ.
. Следовательно, при построении метода Якоби в качестве матрицы ращепления используется диагональ матрицы СЛАУ.
Запишем метод Якоби в координатной форме для  системы общего вида:
системы общего вида:
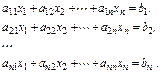
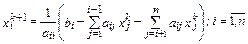 |
Нетрудно убедиться, что метод Якоби в координатной форме
есть не что иное, как разрешение каждого из уравнений системы относительно одной из компонент вектора. Из первого уравнения системы выражается 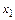 и его значение принимается за значение
и его значение принимается за значение 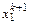 . Из второго уравнения определяется
. Из второго уравнения определяется 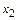 и его значение принимается за
и его значение принимается за 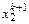 и т. д. Переменные в правой части этих соотношений при этом полагаются равными их значениям на предыдущей итерации.
и т. д. Переменные в правой части этих соотношений при этом полагаются равными их значениям на предыдущей итерации.
Рассмотрим пример системы линейных алгебраических уравнений с разреженной (пятидиагональной) матрицей A (рис. 4.1) и оценим эффективность решения такой системы методом Якоби. Будем хранить матрицуA в виде пяти одномерных массивов g, f, a, b, c. Тогда решаемая система в терминах указанных массивов примет вид
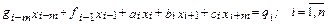 .
. 
В этой записи следует учесть, что отдельные коэффициенты являются нулевыми. В частности 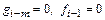 при i=1;
при i=1; 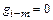 при
при 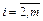 ;
; 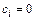 при
при 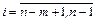 ;
; 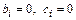 при
при 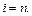



Рис. 4.1. Система с пятидиагональной матрицей
Реализация метода Якоби для такой системы линейных алгебраических уравнений осуществляется просто:
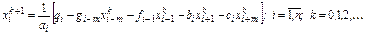
Видно, что для вычисления компоненты вектора решения необходимо выполнить четыре операции умножения и сложения и одну операцию деления. Полное время одной итерации метода Якоби оценивается соотношением
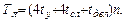
Метод Гаусса–Зейделя.
Решаемую систему запишем в виде
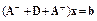 .
.
Итерационная схема Гаусса–Зейделя также следует из этого пред-ставления системы:
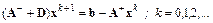 ,
,
или
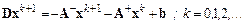 .
.
Последняя форма такого итерационного метода удобна для реа-лизации.
Приведем метод Гаусса–Зейделя к стандартному виду:
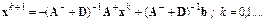
Стандартная форма метода позволяет выписать его итерационную матрицу и провести над ней очевидные преобразования:
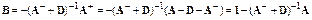 .
.
Матрица расщепления
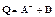
cодержит всю нижнюю треугольную часть матрицы A.
Запишем метод Гаусса–Зейделя в координатной форме для системы общего вида:
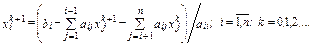
Координатная форма метода Гаусса–Зейделя отличается от координатной формы метода Якоби лишь тем, что первая сумма в правой части итерационной формулы содержит компоненты вектора решения не на k-й, а на (k+1)-й итерации. Но именно это означает, что матрица расщепления метода Гаусса–Зейделя включает не только диагональные члены матрицы A,но и все члены, расположенные ниже главной диагонали.
Оценим, как и ранее, временные затраты метода при решении тестовой задачи - СЛАУ с пятидиагональной матрицей. Реализация метода Гаусса–Зейделя для такой системы:
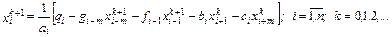
позволяет констатировать, что временные затраты на итерации метода
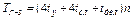
оказываются такими же, как и в методе Якоби. Ключ к пониманию более высокой эффективности метода Гаусса–Зейделя - количество итераций, требующееся для получения решения с заданной точностью. Более высокая сходимость к решению в методе Гаусса–Зейделя достигается за счет выбора матрицы расщепления, лучше аппроксимирующей матрицу A.
