Оптимальные решения в играх двух лиц с нулевой суммой

Для решения игры двух лиц с нулевой суммой предлагается критерий минимакса – максимина.Этот критерий является наиболее осторожным, поскольку основывается на выборе наилучшей из наихудших возможностей. Рассмотрим игру с матрицей

Стратегии	В1	В2	…	Вn	αi
А1	a11	a12	…	a1n	α1
А2	a21	a22	…	a2n	α2
…	…	…	…	…	…
Аm	am1	am2	…	amn	αm
bj	b1	b2	…	bn

Каждый игрок стремится себе обеспечить максимально возможный выигрыш при любых действиях противника. Найдем оптимальные стратегии для каждого из игроков.

Игрок А играет против игрока В и считает, что какую бы стратегию он ни выбрал, игрок В постарается выбрать стратегию, минимизирующую его проигрыш, и тем самым минимизирующую выигрыш игрока А, т.е.

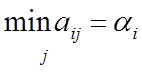, (по строкам).

За оптимальную игрок А разумеется, выберет стратегию, для которой выигрыш будет максимальным, т.е.

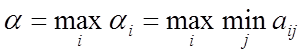
Выбранная игроком А стратегия называется максиминной стратегией, а соответствующее ей значение выигрыша α называется нижней ценой игры. Это гарантированный выигрыш игрока А при любой стратегии игрока В.

В итоге, если игрок А придерживается своей максиминной стратегии, его выигрыш в любом случае будет не меньше нижней цены игры, т.е.

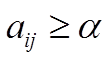
Игрок В считает, что какую бы стратегию он ни выбрал, игрок А выберет стратегию, максимизирующую его выигрыш, значит, из осторожности он должен выбрать максимальный свой проигрыш

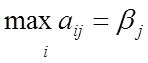, (по столбцам).

Далее, среди этих стратегий игрок В должен выбрать в качестве оптимальной такую стратегию, для которой его проигрыш b_j минимален, т.е.

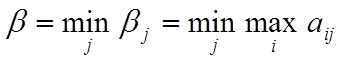
Выбранная игроком В стратегия называется минимаксной стратегией, а соответствующее ей значение проигрыша b называется верхней ценой игры. Это гарантированный минимальный проигрыш игрока В при любой стратегии игрока А.

В итоге, если игрок В придерживается своей минимаксной стратегии, его проигрыш в любом случае будет не больше верхней цены игры, т.е.

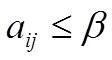
Из условий, определяющих критерий минимакса – максимина, следует

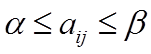
Игра, для которой α = b называется игрой с седловой точкой.

Решением игры называется пара 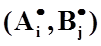оптимальных стратегий, соответствующих седловой точке.Выигрыш a_ij, соответствующий решению игры называется ценой игры (ν), причем ν = α = b.

Решение игры обладает следующим свойством (устойчивостью): если один из игроков придерживается своей оптимальной стратегии, то для другого игрока не выгодно отклоняться от своей оптимальной стратегии.

Если игра имеет седловую точку, то есть α = b,то говорят, что она решается в чистых стратегиях

Найдем решение игры примера 1. Платежная матрица игры имеет вид

Стратегии	В1	В2	В3	αi
А1 А2 А3		-1	-2 -1	-2 -1
bj

Нижняя цена игры 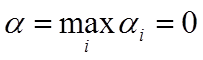, верхняя цена игры 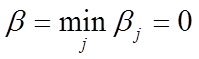. Так как α = b,то игра имеет седловую точку. Решение игры (А₃,В₃), цена игры ν =0.