Тема 10.3.: Решение задач

План занятия.

1) Сторона основания правильной треугольной пирамиды равна 2см, боковое ребро 6см. Определить объем. Ответ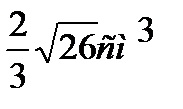

2) Сторона основания правильной четырехугольной призмы равна 3см, боковое ребро 10см. Определить объем. Ответ 90см³.

3) В правильной четырехугольной пирамиде высота 6м, боковое ребро 10м. Найти объем. Ответ 256м³.

4) Боковые ребра треугольной пирамиды взаимно перпендикулярны и каждое равно 3см. определить объем. Ответ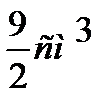

Решить в аудитории задачи

Задача №1. В правильной треугольной пирамиде боковое ребро равно 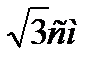и наклонено к плоскости основания под углом 60⁰. Определить объем пирамиды. Ответ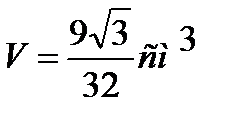

Задача №2. Определить объем правильной четырехугольной усеченной пирамиды, если ее диагональ равна 9см, а стороны оснований 7см и 5см. Ответ 109см³.

Домашнее задание

Задача №1. В правильной треугольной пирамиде сторона равна 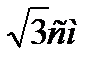и наклонена к плоскости основания под углом 60⁰. Определить объем пирамиды. Ответ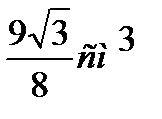

Задача №2. В треугольной прямой призме стороны основания 37см, 13см, 30ми. Площадь боковой поверхности 480см². Найти объем призмы. Ответ 1080см³.

Тема 10.4.: Объем цилиндра.

формула объема цилиндра.

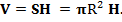
Решение задачи

Задача №1. Один цилиндр имеет высоту 2,4м и α=4м, другой h=1,2м, d=2м. Найти отношение их объемов. Ответ 8м³.

1) Объем тетраэдра, если а (сторона основания) равна 1см, h=6см. Ответ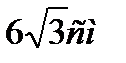

2) Объем правильной четырехугольной призмы, если диагональ призмы 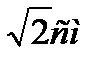и наклонена к плоскости основания под углом 45⁰. Ответ 1см³.

Н=8см. Н=12см.

R=6см. α=30⁰

Sбок.=? ℓ=?

Задача №3. 25м медной проволоки весит 100,7г. Найти диаметр проволоки. (плотность меди 8,9). Ответ ≈0,75мм.

3. Задача №4. В цилиндр вписан прямоугольный параллелепипед диагональ которого 24см и составляет угол 60⁰. Найти объем цилиндра. Ответ 432πсм³.

4. Задача №5. Площадь боковой поверхности цилиндра 16πсм², длина окружности 4πсм. Найти объем. Ответ 16πсм³.

Тема 10.6: Объем конуса, усеченного конуса.

План занятия.

Формула нахождения объема конуса, усеченного конуса.

Решение задач на применение формул.

а) Решение задач №1, 2, 3.

б) Опрос по моделям (определение геометрических тел, их элементов, формулы Sбок., Sполн., V)

R-радиус основания конуса, Η-высота:

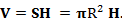
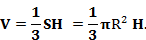
R, r- радиусы верхнего и нижнего оснавания усеченного конуса, б h-высота:

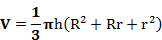
Решить задачи

Задача №1. Площадь основания конуса 9πсм². Полная поверхность 24πсм². Определить

V конуса.

Задача №2. Высота конуса равна 15м. Объем равен 320πм³. Определить Sполн.

Ответ 200πм².

Задача №3. Высота усеченного конуса равна 3см, радиус одного основания вдвое больше другого, а образующая наклонена к основанию под углом 45⁰. Найти объем.

Ответ 63πсм³.

Домашнее задание

Задача №1. Радиусы оснований усеченного конуса 20см и 10см. Образующая наклонная к плоскости основания под углом 45⁰. Определить объем. Ответ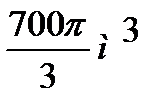

Задача №2. Объем усеченного конуса равен 584см³. Радиусы оснований 10см и 7см. Определить высоту. Ответ 8см.