Метод наименьших квадратов. Метод наименьших квадратов

Введение

Метод наименьших квадратов

Задача метода состоит в том, чтобы по точкам, полученным опытным путем и связанным некоторой функциональной зависимостью, найти эмпирические (опытные) формулы общего вида, наилучшим образом согласующиеся с опытными данными. Эти формулы являются гипотезами, так как они дают возможность вычислять промежуточные значения и прогнозировать изменения наблюдаемого в опыте процесса.

Полный факторный эксперимент первого порядка

Первый этап планирования эксперимента для получения линейной модели основан на варьировании факторов на двух уровнях. В этом случае, если число факторов известно, можно сразу найти число опытов, необходимое для реализации всех возможных со­четаний уровней факторов. Простая формула, которая для этого используется: N=2^k, где N – число опытов, k – число факторов, 2 – число уровней. В общем случае эксперимент, в котором реализуются все­возможные сочетания уровней факторов, называется полным факторным экспериментом. Если число уровней каждого фактора равно двум, то имеем полный факторный экспе­римент типа 2^k.

Ортогональный центральный композиционный план второго порядка

Планы второго порядка позволяют получить математическое описание в виде полной квадратичной модели, содержащей кроме основных эффектов b_i все парные взаимодействия b_ij и квадратичные эффекты b_ii. Подобные планы применяют, как правило, либо в том случае, когда использование планирования первого порядка не позволило получить адекватную регрессионную модель, и выяснилась необходимость ее усложнения, либо если заранее известно, что объект исследования обладает существенными нелинейными свойствами. Центрально–композиционные планы (ЦКП) любой модификации состоят из трех частей. Первая часть – основа или ядро плана – это ПФЭ 2^k или ДФЭ 2^k–p, где k – количество неизвестных коэффициентов регрессии, p = 0,1,2. При этом требуется, чтобы ядро плана обеспечивало раздельную оценку коэффициентов регрессии и всех парных взаимодействий.

Задание №1

Метод наименьших квадратов

1. Вывод формул для коэффициентов линейной регрессии методом наименьших квадратов.

2.Определить коэффициенты линейной регрессии методом наименьших квадратов.

3. Необходимо найти , которые наилучшим образом представляют результат эксперимента по методу наименьших квадратов. Оценки коэффициентов регрессии определяется из условия:

4 . Построить зависимости R от T.

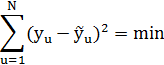
Для определения из условия min

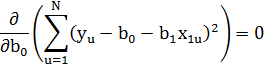
Для решения системы уравнения используется метод Крамера.

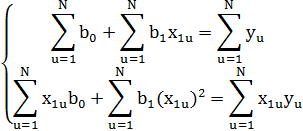
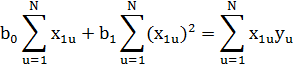
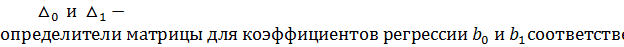
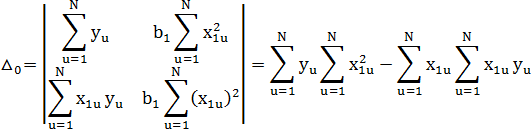
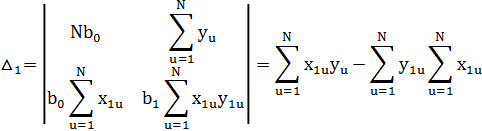
Формулы для нахождения неизвестных переменных по методу Крамера :

;

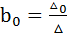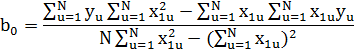
Вычислим все суммы , подставляя численные значения в формулу b₀ и b_1.

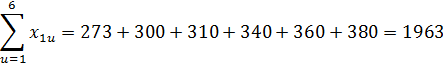
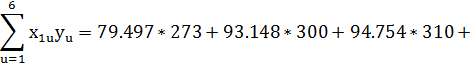
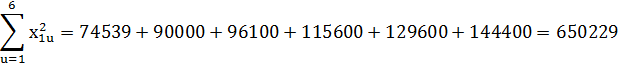
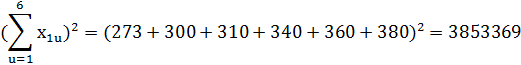
Находим численные значения коэффициентов регрессии:

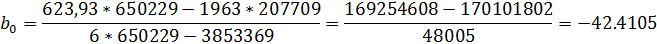
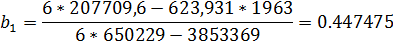
Определяем сопротивление проводника по формуле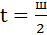

C⁰

T=674.5 K

Y=R=b₀+x*b₁=-17.65+440.5*0.18=259.4116Oм

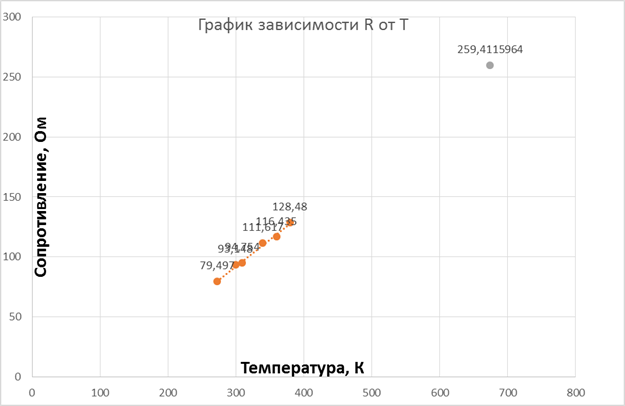
График зависимости R от T

Задание №2.