Контрольная карта медиан и размахов (Ме-R-карта)

Пример.Данные об отклонениях веса от номинала ,выраженные в граммах , найдены в результате последовательно произведённых взвешиваний резиновых деталей в 20 подгрупп по пять элементов. Определить статистическую управляемость процесса изготовления этих деталей в случае , когда по каким-либо причинам необходимо минимизировать вычислительные работы (табл. 12)

Решение.1.Исходя из того , что по условию необходимо минимизировать вычислительные работы , следует воспользоваться картой медиан и размахов (Ме-R-карта) .

Анализ результатов взвешиваний изделий.Табл. 12

№	Данные	Расчёт
Значения	Ранжированные значения	R
							Me
	-12		-15	-8		-15	-12	-8
		-8		-1		-8	-1
		-14		-6		-14	-6
	-3		-15	-5		-15	-5	-3
			-8	-3		-8	-3
					-2	-2
	-13	-14	-11			-14	-13	-11
			-12		-6	-12	-6
	-1	-11		-7	-12	-12	-11	-7	-1
		-11		-12		-12	-11
	-14		-10	-1	-14	-14	-14	-10	-1
	-1	-6	-3		-7	-7	-6	-3	-1
			-2			-2
		-11	-13			-13	-11
				-3	-15	-15	-3
	-3	-1		-13		-13	-3	-1
	-9					-9
	-9	-12	-4	-3	-14	-14	-12	-9	-4	-3
		-2	-9		-9	-9	-9	-2
				Сумма	-13
	Среднее	-0,65			20,9

2. Данные для построения карты подобного типа собираем в подгруппы с нечётным количеством переменных , что облегчает процесс нахождения медианы. Для этого достаточно проранжировать (расположить по возрастанию) значения каждой мгновенной выборки отдельно (табл.12). Значения , оказавшиеся в среднем третьем столбце , и будут медианами. Кроме того ,по этой же таблице легко рассчитать и размахи как разницу между максимальными значениями, записанными в пятом столбце , и минимальными из первого столбца R1= 11-(-15) =26 ; R2= 14 – (-8) = 22 и т.д. , заполняя последовательно весь столбец R табл.12.

3. Рассчитываем среднее значение размаха :

Rср. = 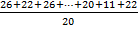= 20.9

4. Рассчитываем среднее значение медианы :

Ме 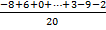= (-0,65)

5.Рассчитываем контрольные пределы и средние линии для верхней части Ме – R –карты , где А4 = 0,69 , так как n = 5

UCL= -0.65 + 0.69 * 20.9 =13.77 LCL= -0.65 – 0.69 * 20.9 = (-15.07) CL= (-0.65)

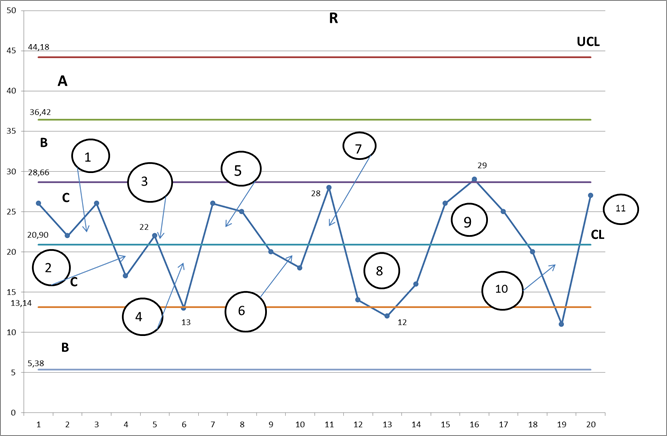
6.Расчитываем контрольные пределы и средние линии для нижней части Хср. – R – карты , где D3 = 0 , D4 = 2.114 , так как n = 5

UCL = 2.114 * 20.9 =44.18LCL=0*20.9 = 0 CL= 20.9

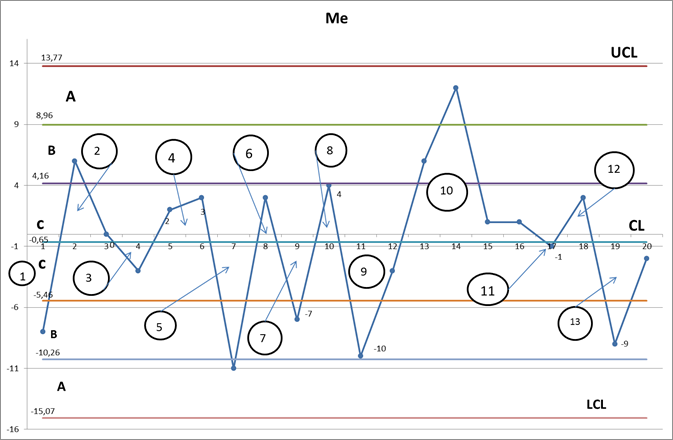
Наносим полученные контрольные границы на контрольную карту (рис.11)

7.Поскольку наблюдения имеют временную последовательность , можно проанализировать процесс на наличие внешнего воздействия . Для определения зон используем графический метод : делим расстояние от средней линии до верхнего контрольного предела (3δ) на три равных отрезка (по δ) и откладываем такие же отрезки от средней линии до нижнего контрольного предела или сколько получиться до нулевой линии. Далее от намеченных концов отрезов проводим горизонтальные линии , обозначающие границы зон. Поскольку точек , имеющих спорное местоположение , нет , точных координат границ зон можно не находить.

8.На Ме – графике 13 зон , а на R – графике -11 при норме для 20 точек от 6 до 15 , следовательно , по данному критерию специальных причин вариаций не обнаружено.

Анализ на наличие критериев для особых причин табл.11

№	Критерий	Ме –график	R– график
наличие	место	наличие	место
	Одна точка вне зоны А	нет	------	нет	----
	Девять точек подряд в зонеС или по одну сторону от центральной линии	нет	-----	нет	-----
	Шесть возрастающих или убывающих точек подряд	нет	-----	нет	----
	Четырнадцать попеременно возрастающих и убывающих точек	нет	-----	нет	----
	Две из трёх последовательных точек в зоне А или вне её	нет	-----	нет	----
	Четыре из пяти последовательных точек в зонеB или дальше от центральной лини	нет	-----	нет	----
	Пятнадцать последовательных точек в зонеС выше и ниже центральной линии	нет	-----	нет	----
	Восемь последовательных точек по обеим сторонам центральной линии и ни одной в зоне С	нет	-----	нет	----

Поскольку не было обнаружено критериев , сигнализирующих о наличии особых причин , можно утверждать , что процесс находиться в статистически регулируемом состоянии.