А если на упругое твердое тело действует несколько внешних сил?
Представим себе балку, шарнирно опертую по краям (см., например, рис. 15.1) и нагруженную силами 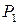 ,
, 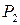 , …,
, …, 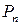 . Пусть
. Пусть 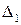 ,
, 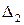 , …,
, …, 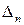 перемещения точек приложения этих сил по направлениям их действия. Тогда, согласно теореме Клапейрона:
перемещения точек приложения этих сил по направлениям их действия. Тогда, согласно теореме Клапейрона:
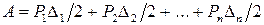 .
.
Важно отметить, что, записывая выражение для упругой работы внешних сил, мы принимаем во внимание только активные силы и совсем не учитываем силы реактивные – реакции опор. Поскольку перемещения на опорах отсутствуют, работа реакций всегда равна нулю.
15.3. Какая сила и какое перемещение называются обобщенными?
Внешняя нагрузка, действующая на балку, обычно представляет собой группу сил. Упругую работу группы сил по теореме Клапейрона можно записать в виде:
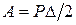 ,
,
где множитель P зависит только от сил этой группы и называется обобщенной силой, а  зависит от перемещений и называется обобщенным перемещением.
зависит от перемещений и называется обобщенным перемещением.
Таким образом, под обобщенной силой будем понимать любую нагрузку (сосредоточенные силы, моменты, распределенную нагрузку), а под обобщенным перемещением – тот вид перемещения, на котором обобщенная сила производит работу.

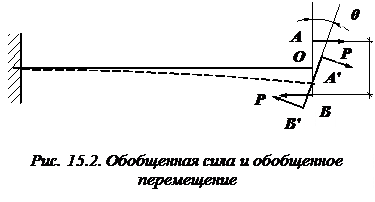
Пусть, например, группа сил состоит из двух равных постоянных сил P, образующих пару. Момент этой пары (рис. 15.2) равен 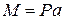 .
.
Допустим, что в результате деформации системы элемент AB повернулся на угол 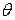 . Пути, пройденные точками приложения сил P по направлениям их действия, соответственно равны
. Пути, пройденные точками приложения сил P по направлениям их действия, соответственно равны 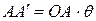 и
и 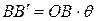 .
.
Суммарная работа обеих сил:
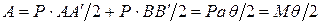 .
.
Следовательно, если обобщенной силой является момент M, то обобщенным перемещением – угол поворота 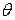 .
.
15.4. Как определяется работа внутренних сил?
Если нагруженное тело находится в равновесии, то внутренние силы (силы упругости) равны по значению внешним силам и противоположны им по направлению, поскольку они препятствуют развитию деформации. Поэтому работа внутренних сил U, с учетом их направления по отношению к деформации, всегда является отрицательной.
При этом, очевидно, что работа внешних сил равна взятой с обратным знаком работе внутренних сил, то есть 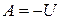 .
.
Пусть элемент стержня длиной 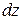 испытывает растяжение. Действие отброшенных частей стержня на рассматриваемый элемент заменим продольными «растягивающими» силами N, направленными от сечения. По отношению к элементу они являются как бы внешними. Тогда «вызываемое» ими удлинение элемента равно:
испытывает растяжение. Действие отброшенных частей стержня на рассматриваемый элемент заменим продольными «растягивающими» силами N, направленными от сечения. По отношению к элементу они являются как бы внешними. Тогда «вызываемое» ими удлинение элемента равно:
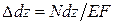 .
.
Действие рассматриваемого элемента на отброшенные нами части стержня представляет собой для рассматриваемого элемента как бы внутренние усилия. Элементарная работа именно этих, постепенно увеличивающихся, внутренних продольных сил, противодействующих развитию удлинения, согласно теореме Клапейрона, равна:
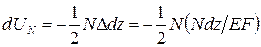 .
.
Теперь вычислим элементарную работу внутренних перерезывающих сил  при чистом сдвиге. Напомним, что в этом случае считается, что касательные напряжения равномерно распределены по всему сечению и определяются по формуле
при чистом сдвиге. Напомним, что в этом случае считается, что касательные напряжения равномерно распределены по всему сечению и определяются по формуле
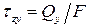 .
.
Абсолютный сдвиг  правого сечения элемента длиной
правого сечения элемента длиной 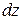 по отношению к левому сечению, с учетом закона Гука, равен:
по отношению к левому сечению, с учетом закона Гука, равен:
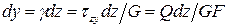 ,
,
тогда
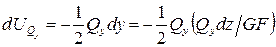 .
.
При поперечном изгибе касательные напряжения распределены по сечению неравномерно. В этом случае выражение для элементарной работы внутренних перерезывающих сил может быть представлено в виде:
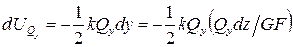 ,
,
где k – коэффициент, зависящий от формы поперечного сечения стержня. Например, для прямоугольного поперечного сечения 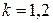 .
.
Определим теперь элементарную работу внутренних усилий при кручении. Поворот правого сечения элемента длиной 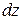 по отношению к левому сечению, происходящий под действием внешних по отношению к нему крутящих моментов
по отношению к левому сечению, происходящий под действием внешних по отношению к нему крутящих моментов 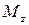 , согласно закону Гука,равен:
, согласно закону Гука,равен:
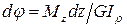 .
.
Тогда элементарная работа внутренних крутящих моментов на этом же угле поворота определяется по формуле
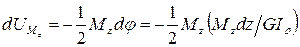 .
.
Пусть теперь элемент стержня длиной 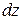 испытывает чистый изгиб. И пусть его правое поперечное сечение повернется на угол
испытывает чистый изгиб. И пусть его правое поперечное сечение повернется на угол 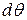 по отношению к левому сечению. Значение этого угла поворота мы определили ранее (см. беседу 7). Оно равно:
по отношению к левому сечению. Значение этого угла поворота мы определили ранее (см. беседу 7). Оно равно:
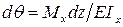 .
.
Тогда внутренние изгибающие моменты совершат на этом угле поворота следующую элементарную работу:
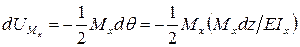 .
.
При одновременном растяжении, кручении и прямом поперечном изгибе стержня (с учетом того, что работа каждого из внутренних усилий на перемещениях, вызываемых остальными усилиями, равна нулю) получим следующее выражение для элементарной работы внутренних сил:
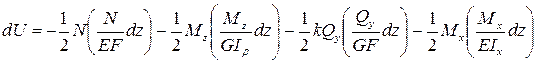 .
.
Интегрируя последнее выражение по всей длине стержня, окончательно будем иметь:
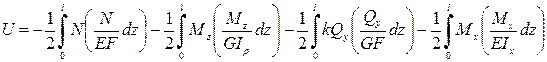 .(15.4)
.(15.4)
15.5. Как формулируется принцип возможных перемещений?
Этот принцип в 1788 г. был сформулирован для абсолютно твердых тел французским ученым Жозефом Луи Лагранжем (Lagrange,1736 – 1813 гг.) и впервые применен к деформируемым телам Пуассоном в 1833 г.
Принцип возможных перемещений формулируется следующим образом: если система находится в равновесии под действием приложенной к ней нагрузки, то сумма работ внешних и внутренних сил на всяком бесконечно малом возможном перемещении точек системы, допускаемых связями, равна нулю:
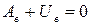 ,
,
где 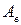 – возможная работа внешних, а
– возможная работа внешних, а 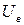 – возможная работа внутренних сил.
– возможная работа внутренних сил.
Заметим, что в процессе совершения системой возможного перемещения значения и направления внешних и внутренних сил считаются неизменными, то есть такими же, как и в исходном состоянии.
Поэтому возможная работа внешних и внутренних сил определяется простым произведением соответствующих сил и перемещений, то естьв отличие от выражения для упругой работы в выражении для возможной работы коэффициента  нет.
нет.
Учитывая принятое в сопротивлении материалов допущение о малости деформаций, а также линейную зависимость деформаций от нагрузок, в качестве возможных перемещений можно принимать и конечные упругие перемещения, вызванные любым видом внешней нагрузки и происходящие без нарушения связей.
15.6. Как формулируется теорема Бетти (теорема о взаимности работ)?
Эта теорема, доказанная в 1872 г. итальянским ученым Энрико Бетти (Betti, 1823 – 1892 гг.), формулируется следующим образом: возможная работа сил первого состояния на соответствующих перемещениях, вызванных силами второго состояния, равна возможной работе сил второго состояния на соответствующих перемещениях, вызванных силами первого состояния. Приведем доказательство этой теоремы.
Наметим на балке две точки 1 и 2 (рис. 15.3, а). Приложим статически в точке 1 силу 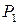 . Она вызовет в этой точке прогиб
. Она вызовет в этой точке прогиб 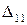 , а в точке 2 –
, а в точке 2 – 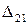 . Для обозначения перемещений мы используем два индекса. Первый индекс означает место перемещения (где), а второй – причину, вызывающую это перемещение (от какого усилия).
. Для обозначения перемещений мы используем два индекса. Первый индекс означает место перемещения (где), а второй – причину, вызывающую это перемещение (от какого усилия).
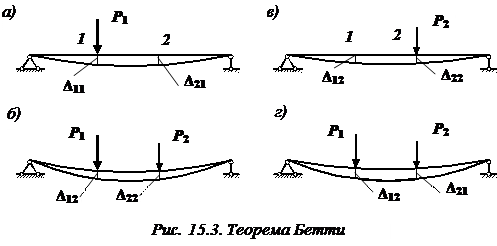
Так, например,  означает прогиб балки в точке 2от нагрузки
означает прогиб балки в точке 2от нагрузки 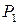 .
.
После того, как закончен рост силы 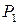 , приложим в точке 2 к деформированному состоянию балки статическую силу
, приложим в точке 2 к деформированному состоянию балки статическую силу 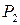 (15.3, б). Балка получит дополнительные прогибы:
(15.3, б). Балка получит дополнительные прогибы: 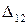 в точке 1 и
в точке 1 и 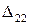 в точке 2.
в точке 2.
Составим выражение для работы, которую совершают эти силы на соответствующих им перемещениях:
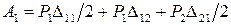 .
.
Здесь первое и третье слагаемые представляют собой упругие работы сил 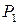 и
и 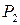 . Согласно теореме Клапейрона, они имеют коэффициент
. Согласно теореме Клапейрона, они имеют коэффициент  . У второго слагаемого этого коэффициента нет, поскольку сила
. У второго слагаемого этого коэффициента нет, поскольку сила 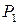 своего значения не изменяет и совершает возможную работу на перемещении
своего значения не изменяет и совершает возможную работу на перемещении 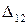 , вызванном другой силой
, вызванном другой силой 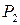 .
.
Изменим теперь порядок нагружения балки. Сначала прикладываем к балке силу 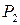 , а затем
, а затем 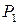 (рис. 15.3, в, г).
(рис. 15.3, в, г).
Тогда
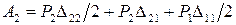 .
.
Очевидно, что 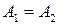 . Из этого равенства и следует теорема Бетти:
. Из этого равенства и следует теорема Бетти:
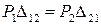 .
.
Заметим, что теорема Бетти справедлива как для случая внешних, так и для случая внутренних сил.
15.7. А как формулируется теорема о взаимности перемещений?
Пусть 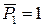 и
и 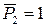 . Тогда, с учетом принятого нами обозначения перемещения от единичной силы, будем иметь:
. Тогда, с учетом принятого нами обозначения перемещения от единичной силы, будем иметь:
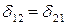 .
.
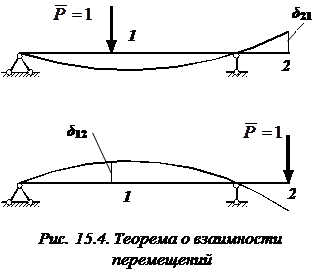
Это выражение носит название теоремы о взаимности перемещений. Она была доказана в 1864 г. Максвеллом и формулируется следующим образом:
Перемещение точки приложения первой единичной силы, вызванное действием второй единичной силы, равно перемещению точки приложения второй единичной силы, вызванному действием первой единичной силы (рис. 15.4).
