Критерии грубых погрешностей

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

Уфимский государственный нефтяной технический университет

Кафедра автоматизации технологических процессов и производств

Курсовая работа

по теме:

«Обработка результатов измерений»

Вариант 20/3

Выполнил: ст. гр. БАГ-11-02 И.И.Сибагатуллин

Проверил: Э.А.Шаловников

Уфа 2013

Содержание

1. Обработка результатов прямых измерений………………………………..…3

1.1. Точечная оценка………………………………………………………...……3

1.2. Критерии грубых погрешностей………………………….…………………3

1.3. Интервальная оценка……………………………….………………………...6

1.4. Интервальная оценка среднего квадратического отклонения……….……6

1.5. Результаты измерения………………………………………………………..7

2. Обработка результатов косвенных видов измерений………………………..8

2.1. Методика обработки результатов измерений аргумента X2………………8

2.1.1. Точечная оценка……………………………………………………..8

2.1.2. Критерии грубых погрешностей……………………………………8

2.1.3. Интервальная оценка………………………………………………..9

2.1.4. Интервальная оценка среднего квадратического отклонения……9

2.1.5. Результаты измерения……………………………...………………10

2.2. Методика обработки косвенных видов измерений………………….……10

2.3. Результаты расчёта………………………………………………………….11

3. Методика расчёта статистических характеристик погрешностей СИ в эксплуатации. Определение класса точности………………………………..12

3.1. Обработка результатов……………………………………………………...12

3.2. Результаты расчёта………………………………………………………….13

Приложение………………………………………………………………………14

Обработка результатов прямых измерений

Исходные данные:

Результаты измерения сопротивления резистора (кОм):

8.821

8.795

7.695

8.751

8.821

8.797

8.781

8.807

8.789

8.731

8.605

Обработка результатов прямых равноточных измерений:

Точечная оценка

Ранжированный ряд, n=11.

7.695

8.605

8.731

8.751

8.781

8.789

8.795

8.797

8.807

8.821

8.821

1. Среднее арифметическое (оценка математического ожидания):

;

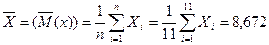2. Проверим правильность вычисления :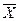

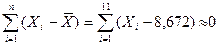, значит вычисления произведены верно.

3. Найдем среднее квадратическое отклонение:

а) Оценка с.к.о. отдельного результата наблюдения (формула Бесселя):

;

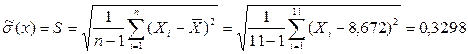б) Оценка с.к.о. среднего арифметического :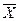

;

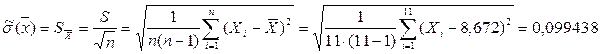Критерии грубых погрешностей

Так как количество измерений n=11, то используется критерий Грабса (Романовского или ν-критерий):

;

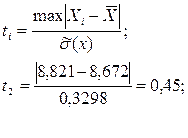
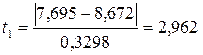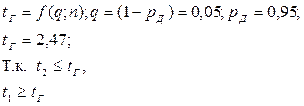
X_min = 7,695 содержит грубую ошибку, её исключаем, расчёт повторяем:

Точечная оценка при исключении X_min = 7,695

Ранжированный ряд, n=10.

8.605

8.731

8.751

8.781

8.789

8.795

8.797

8.807

8.821

8.821

1. Среднее арифметическое (оценка математического ожидания)6

;

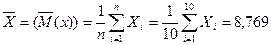2. Проверим правильность вычисления :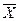

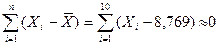, значит вычисления произведены верно.

3. Найдем среднее квадратическое отклонение:

а) Оценка с.к.о. отдельного результата наблюдения (формула Бесселя):

;

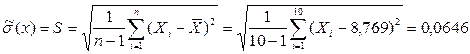б) Оценка с.к.о. среднего арифметического :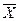

;

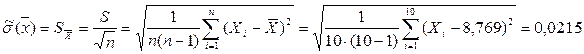Критерии грубых погрешностей при исключении X_min = 7,695

Так как количество измерений n=10, то используется критерий Грабса (Романовского или ν-критерий):

;

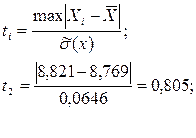
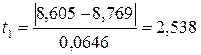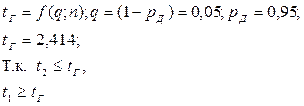
X_min = 8,605 содержит грубую ошибку, её исключаем, расчёт повторяем:

Точечная оценка при исключении X_min = 8,605

Ранжированный ряд, n=9.

8.731

8.751

8.781

8.789

8.795

8.797

8.807

8.821

8.821

1. Среднее арифметическое (оценка математического ожидания):

;

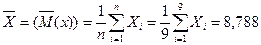2. Проверим правильность вычисления :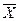

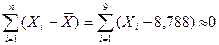, значит вычисления произведены верно.

3. Найдем среднее квадратическое отклонение:

а) Оценка с.к.о. отдельного результата наблюдения (формула Бесселя):

;

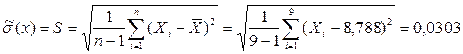б) Оценка с.к.о. среднего арифметического :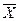

;

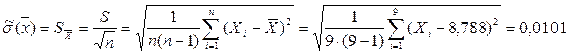Критерии грубых погрешностей при исключении X_min = 8,605

Так как количество измерений n=9, то используется критерий Грабса (Романовского или ν-критерий):

;

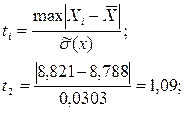
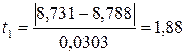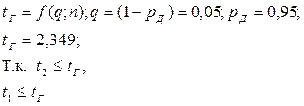
Не содержит грубую ошибку, расчёт продолжаем.

Интервальная оценка

Оценка доверительного интервала математического ожидания :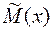
;

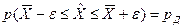По формуле Петерса:

;

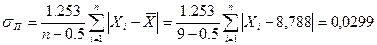Поскольку 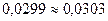, то это нормально распределение.

p_Д =0,95;

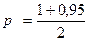= 0,975;

t = f ( p) = 1,96;

;
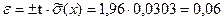