Модель направленных отрезков
Задачи механики и физики используют модели, элементами которых являются объекты, характеризуемые величиной действия в заданном направлении. Такими объектами являются силы, скорости, ускорения и др. Над этими объектами определены операции сложения по определенному закону и умножения на число. При этом как сами объекты, так и результаты операции над ними не зависят от параллельного переноса в пространстве. В качестве геометрической модели или знаковой системы для определения этих объектов удобно использовать направленные отрезки, которые имеют заданное направление и длину. Сформулируем нашу первую задачу.
А. Построить систему свойств (аксиоматику), достаточную для описания модели направленных отрезков с операциями сложения и умножения на число.
Решение сформулированной задачи состоит из двух частей: 1) в определении направленных отрезков, определении указанных операций, доказательстве основных свойств этих операций и 2) указании критерия, согласно которому проверяется, что сформулированных свойств достаточно для описания модели.
Вначале определим операции и построим систему свойств (аксиом). Направленный отрезок 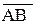 есть отрезок AB заданной длины, направленный параллельно некоторой прямой «l» причем порядок пары точек означает, что точка А - начало, В - конец направленного отрезка.
есть отрезок AB заданной длины, направленный параллельно некоторой прямой «l» причем порядок пары точек означает, что точка А - начало, В - конец направленного отрезка.
Для простоты будем направленные отрезки обозначать так же одной буквой 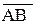 =
=  и т.д.
и т.д.
Так как направление и длина направленного отрезка не зависит от параллельного переноса, то направленный отрезок изображает класс направленных отрезков, совместимых параллельными переносами. Этот факт будем называть инвариантностью направленного отрезка относительно параллельного переноса.
На множестве направленных отрезков  ,
, 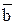 ,
, 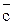 , ... определим операции сложения и умножения на действительное число и установим свойства этих операций.
, ... определим операции сложения и умножения на действительное число и установим свойства этих операций.
Суммой направленных отрезков  и
и 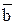 назовем направленный отрезок
назовем направленный отрезок 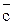 =
=  +
+ 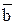 , который имеет то же начало, что и
, который имеет то же начало, что и  и тот же конец, что и
и тот же конец, что и 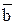 , если начало отрезка
, если начало отрезка 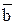 параллельным переносом совместить с концом
параллельным переносом совместить с концом  , рис 4 (а).
, рис 4 (а).
Учитывая инвариантность направленного отрезка относительно параллельного переноса, заключаем, что 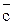 является направленной диагональю параллелограмма, построенного на сторонах
является направленной диагональю параллелограмма, построенного на сторонах  и
и 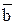 , рис. 4 (b). Правило
, рис. 4 (b). Правило
 |
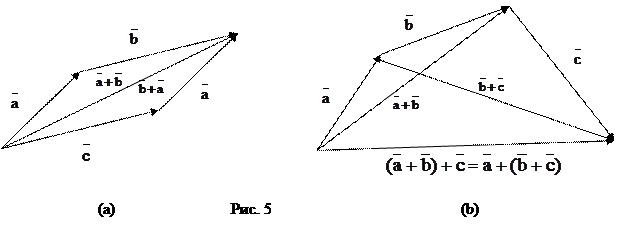
сложения (а) называется правилом треугольника, а правило сложения (b) - правилом параллелограмма.
Сложение обладает свойствами:
1. "  и
и 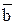
 +
+ 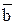 =
= 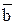 +
+ 
2. "  ,
, 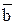 и
и 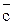 (
(  +
+ 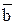 )+
)+ 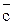 =
=  +(
+( 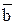 +
+ 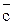 )
)
3. Существует вектор 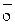 такой, что "
такой, что " 
 +
+ 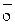 =
=  (
( 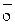 - нулевой вектор)
- нулевой вектор)
4. "  $ «-
$ «-  » такой, что
» такой, что  +(-
+(-  )=
)= 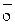 .
.
(«-  » называется противоположенным вектору
» называется противоположенным вектору  ).
).
Свойства 1 и 2 схематично представлены на рис 5(а) и 5(b), соответственно.
Свойство 3 представляет возможность вырождения в точку одного из слагаемых:
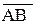 +
+ 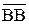 =
= 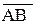 ,
, 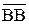 =
= 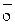
Свойство 4 представляет правило сложения
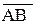 +
+ 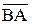 =
= 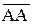 =
= 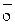 ,
,
в котором естественно считать 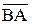 =-
=- 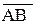 . Длину направленного отрезка
. Длину направленного отрезка  будем обозначать |
будем обозначать |  |. Очевидно, что |
|. Очевидно, что | 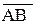 | = |
| = | 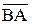 |.
|.
Операция умножения отрезка  на число a определяет направленный отрезок
на число a определяет направленный отрезок 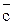 =a
=a  . Длина |
. Длина | 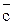 |= |a| |
|= |a| |  |; направление
|; направление 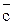 то же, что и у отрезка
то же, что и у отрезка  , если a>0, и обратное, если a<0.
, если a>0, и обратное, если a<0.
Свойства операции умножения:
1. " 
 ·1=
·1=  .
.
2. " a, bÎR и "  a ( b
a ( b  ) = ( a b )
) = ( a b )  .
.
3. " aÎR и "  ,
, 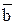 a (
a (  +
+ 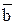 ) = a
) = a  + a
+ a 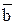 .
.
4. " a, bÎR и "  (a+b)
(a+b)  = a
= a  + b
+ b  .
.
Доказательство восьми свойств сложения и умножения на число направленных отрезков можно найти в школьных учебниках, и мы их опускаем.
Теперь сформулируем понятие вектора.
Определение.
Направленные отрезки с операциями сложения по правилу треугольника (параллелограмма) и умножения на число называются векторами.
В силу инвариантности направленных отрезков относительно параллельного переноса заключаем, что: 1) вектор - это класс направленных отрезков, определяемый всеми параллельными переносами любого из его представителей; 2) свойства операций сложения векторов и умножения на число так же инвариантны относительно параллельного переноса.
