Теоремы о равносильных уравнениях
Теорема 1.Если в уравнении f1(x)=g1(x) выполнить тождественное преобразование выражений f1(x) или (и) g1(x), по формуле, не меняющей область определения данного уравнения D, то получится уравнение f2(x)=g2(x), равносильное данному уравнению на множестве D.
Теорема 2.Если к обеим частям уравнения f(x)=g(x) с областью определения D прибавить одно и то же выражение 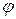 (х), которое определено при всех значениях
(х), которое определено при всех значениях 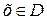 , то получится уравнение
, то получится уравнение 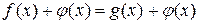 , равносильное данному на множестве D.
, равносильное данному на множестве D.
Следствие.Уравнения 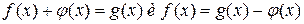 равносильны.
равносильны.
Например, уравнения 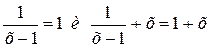 равносильны, а уравнения
равносильны, а уравнения 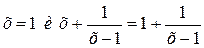 не являются равносильными. Причина не равносильности в том, что выражение
не являются равносильными. Причина не равносильности в том, что выражение 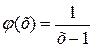 не определено при всех значениях х из области определения данного уравнения.
не определено при всех значениях х из области определения данного уравнения.
Теорема 3.Если обе части уравнения f(x)=g(x) с областью определения D умножить (разделить) на одно и то же выражение 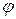 (х), которое определено и не обращается в нуль при всех значениях
(х), которое определено и не обращается в нуль при всех значениях 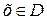 , то получится уравнение
, то получится уравнение 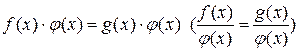 , равносильное данному на множестве D.
, равносильное данному на множестве D.
Например, уравнения х=1 и х∙(х2+1)= х2+1 равносильны, а уравнения х=1 и х∙(х2-1)= х2-1 не равносильны, так как множитель х2-1 обращается в нуль при х=1или х=-1.
Следствие.Если обе части уравнения умножить (разделить) на одно и то же число, отличное от нуля, то получится уравнение, равносильное данному.
Например, приводя уравнение 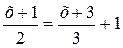 к целому виду умножением его обеих частей на 6, получим уравнение
к целому виду умножением его обеих частей на 6, получим уравнение 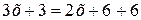 , равносильное данному.Замечание. Решая уравнение
, равносильное данному.Замечание. Решая уравнение 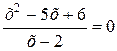 умножением его обеих частей на выражение х-2, получим уравнение
умножением его обеих частей на выражение х-2, получим уравнение 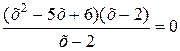 , равносильное данному. Однако следующее преобразование – сокращение дроби приведёт к уравнению
, равносильное данному. Однако следующее преобразование – сокращение дроби приведёт к уравнению  ,не равносильному данному.
,не равносильному данному.
Теорема 4.Если обе части уравнения f(x)=g(x) с областью определения D, для которого выполняется условие f(x)≥0 и g(x)≥0 при 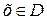 ,возвести в одну и ту же чётную натуральную степень n=2k (
,возвести в одну и ту же чётную натуральную степень n=2k ( 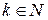 ), то получится уравнение (f(x))2k=(g(x))2k, равносильное данному на области его определения.
), то получится уравнение (f(x))2k=(g(x))2k, равносильное данному на области его определения.
Например, уравнения 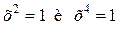 равносильны, а уравнения
равносильны, а уравнения 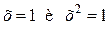 таким свойством не обладают.
таким свойством не обладают.
Замечание. Если неравенства f(x)≥0 и g(x)≥0 выполняются при 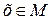 , где М – подмножество области определения данного уравнения, то уравнение f(x)=g(x) равносильно уравнению (f(x))2K=(g(x))2K на множестве М.
, где М – подмножество области определения данного уравнения, то уравнение f(x)=g(x) равносильно уравнению (f(x))2K=(g(x))2K на множестве М.
Таким образом, уравнение f(x)=g(x) равносильно системе 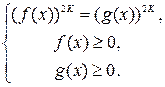
Теорема 5.Если обе части уравнения f(x)=g(x) с областью определения D, для которого выполняется условие f(x)≥0 и g(x)≥0 при 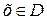 ,возвести в одну и ту же нечётную натуральную степень n=2k+1 (
,возвести в одну и ту же нечётную натуральную степень n=2k+1 ( 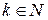 ), то получится уравнение (f(x))2k+1=(g(x))2k+1, равносильное данному на области его определения.
), то получится уравнение (f(x))2k+1=(g(x))2k+1, равносильное данному на области его определения.
Определение.Несколько уравнений называются совокупностью, если ставиться задача об отыскании всех таких значений переменной, каждое из которых является решением хотя бы одного из данных уравнений.
Решением совокупности уравнений является объединение множеств корней уравнений, составляющих совокупность.
Обозначается совокупность с помощью квадратной скобки.
Теорема 6. Уравнение 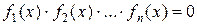 в своей области определения D равносильно совокупности уравнений
в своей области определения D равносильно совокупности уравнений 
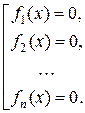
Так, уравнение 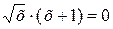 равносильно совокупности уравнений
равносильно совокупности уравнений 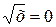 , х+1=0 на промежутке
, х+1=0 на промежутке 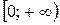 , то есть имеет единственный корень, равный 0.
, то есть имеет единственный корень, равный 0. 
Доказательства теорем 1-6 основано на определении равносильности. Проиллюстрируем ход рассуждений на примере третьей теоремы.
Дано: уравнение f(x)=g(x) с областью определения D (1),
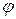 (х) – выражение, которое определено при
(х) – выражение, которое определено при 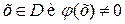 ,
,
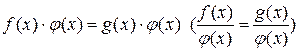 - уравнение (2), полученное умножением (делением) обеих частей данного уравнения на выражение
- уравнение (2), полученное умножением (делением) обеих частей данного уравнения на выражение 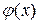 .
.
Доказать: уравнения (1) и (2) равносильны.
Доказательство.
Пусть х1 – корень уравнения (1), тогда f(x1)=g(x1) – истинное числовое равенство, 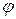 (х1) – число. Значит
(х1) – число. Значит 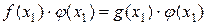 - верное числовое равенство, тогда х1- корень уравнения (2).
- верное числовое равенство, тогда х1- корень уравнения (2).
Обратно. Пусть х2 – корень уравнения (2), следовательно, 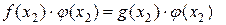 – истинное числовое равенство,
– истинное числовое равенство, 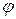 (х2) – число, причем φ(х2) ≠ 0. Тогда f(x2)=g(x2) - верное числовое равенство. Значит,
(х2) – число, причем φ(х2) ≠ 0. Тогда f(x2)=g(x2) - верное числовое равенство. Значит,
х2 - корень уравнения (1).
Таким образом, уравнения (1) и (2) равносильны на множестве D.
***
Корнем n-ой степени из числа а называется число, n-ая степень которого равна а.
Арифметическим корнем n – ой степени из числа а называется неотрицательное число, n – ая степень которого равна а.
Знаком 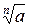 обозначают:
обозначают:
1) арифметический корень n – ой степени из числа а, если n – чётное число;
2) единственное значение корня в случае нечётного n.
Таблица существования корня
| n а | а>0 | а=0 | а<0 |
n=2k( 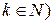 (n-чётное) (n-чётное) | 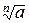 ; - ; - 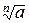 | Не существует | |
N=2k+1( 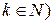 (n-нечётное) (n-нечётное) | 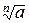 | 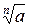 |
***
Логарифмом числа b по основанию а называется показатель степени, в которую следует возвести число а, чтобы получить число b.
Обозначение: loga b,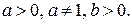
Литература
1. Горнштейн П.И. Экзамен по математике и его подводные рифы / П.И. Горнштейн [и др.] - М., Харьков : ИЛЕКСА, ГИМНАЗИЯ, 1998. – 236 с.
2. Мерзляк А.Г. Алгебраический тренажёр : пособие для школьников и абитуриентов / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир - М. : ИЛЕКСА, 2005. – 320 с.
3. Мерзляк А.Г. Тригонометрия: задачник к школьному курсу / А.Г. Мерзляк, [и др.] - М. : АСТ – ПРЕСС : МАГИСТР S, 1998. – 656 с.
4. Новосёлов С.И. Специальный курс элементарной алгебры / С.И. Новосёлов – М. : Высшая школа, 1965.- 327с.
5. Мордкович А.Г. Алгебра и начала математического анализа. 11 класс, Ч. 1: учебник для общеобр. учр. (профильный уровень) / Мордкович А.Г., П.В. Семёнов. - М. : Мнемозина, - 287 с.
6. Мордкович А.Г. Алгебра и начала математического анализа. 11 класс, Ч. 2: задачник для общеобр. учр. (профильный уровень) / Мордкович А. Г., П.В. Семёнов. - М.: Мнемозина, - 264 с.
7. Олехник С.Н. Уравнения и неравенства. Нестандартные методы решения. 10 – 11 классы: учебно – метод. пособие / С.Н. Олехник, М.К.Потапов, П.И. Пасиченко - М. : Дрофа, 2002. – 192с. - М.: ИЛЕКСА, 2005. – 320 с.
8. Соминский И.С. Элементарная алгебра : дополнительный курс /
И. С. Соминский. – М.: ГИФМЛ, 1963. – 200 с.
