Часть 3. Анализ гармонического состава тока нелинейной цепи в установившемся режиме

В ч. 2 после решения ДУ было найдено время переходного процесса в нелинейной электрической цепи. Гармонический анализ следует проводить в установившемся режиме после окончания переходного процесса.

Произведем гармонический анализ функции с использованием разложения в ряд Фурье:

Для получения непрерывной функции интерполируем зависимость I_j(t_j):

Определим период функции:

Разложение будем производить до 25 гармоники:

Построим итоговую функцию гармонического анализа (рис. 9):

Рисунок 9 - Гармонический анализ тока

Вывод:

В ходе работы были использованы различные методы обработки непрерывных и точечных функций. Интерполяция методом Лагранжа показала низкую эффективность, что обуславливает ее редкое применение в реальных системах обработки данных. Метод Эйлера для решения ДУ оказался достаточно точным для данной задачи.

Контрольный вопрос:

Метод Эйлера для решения дифференциальных уравнений.

В дифференциальное уравнение 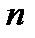–го порядка в качестве неизвестных величин входят функция 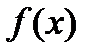и ее первые 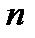производных по аргументу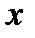

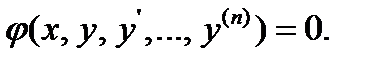(7.1)

Из теории обыкновенных дифференциальных уравнений известно, что уравнение (7.1) эквивалентно системе 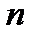уравнений первого порядка

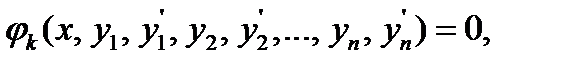(7.2)

где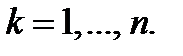

Уравнение (7.1) и эквивалентная ему система (7.2) имеют бесконечное множество решений. Единственные решения выделяют с помощью дополнительных условий, которым должны удовлетворять искомые решения.

Систему (7.2) часто удается представить в каноническом виде, в так называемой форме Коши

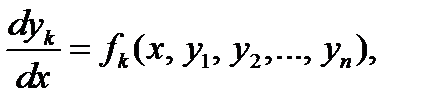(7.3)

где .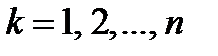

При формулировке задачи Коши система (7.3) дополняется начальными условиями. Рассмотрим задачу Коши для одного уравнения типа (7.3)

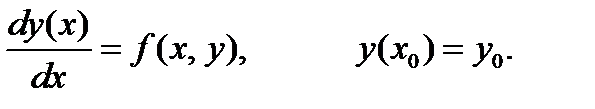(7.4)

В окрестности точки 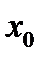функцию 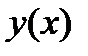разложим в ряд Тейлора

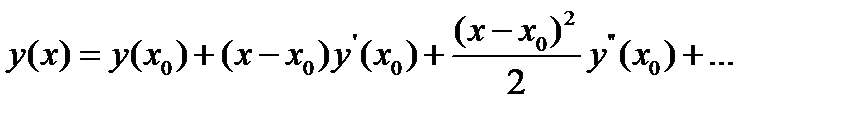(7.5)

который можно применить для приближенного определения искомой функции 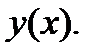В точке 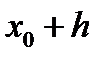при малых значениях 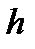можно ограничиться двумя членами ряда (7.5)

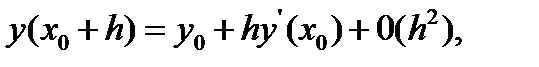(7.6)

где 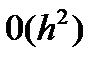– бесконечно малая величина порядка 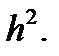Заменим производную 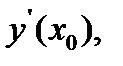входящую в формулу (7.6), на правую часть уравнения (7.4)

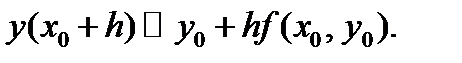(7.7)

Теперь приближенное решение в точке 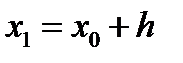можно вновь рассматривать как начальное условие и по формуле (7.7) найти значение искомой функции в следующей точке 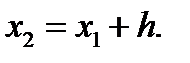В результате получен простейший алгоритм решения задачи Коши, который называется методом Эйлера, или методом ломаных. Последнее название связано с геометрической интерпретацией процесса (рис. 7.1); искомую функцию 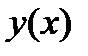заменяем ломаной линией, представляющей собой отрезки касательных к этой функции в узлах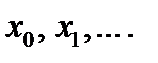

Формула (7.7) может быть получена из других соображений. Заменим производную в левой части уравнения (7.4) приближенным конечно-разностным отношением

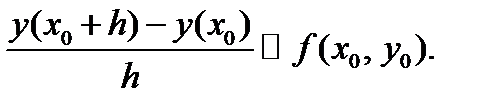
Нетрудно видеть эквивалентность последнего выражения с алгоритмом Эйлера (7.7).

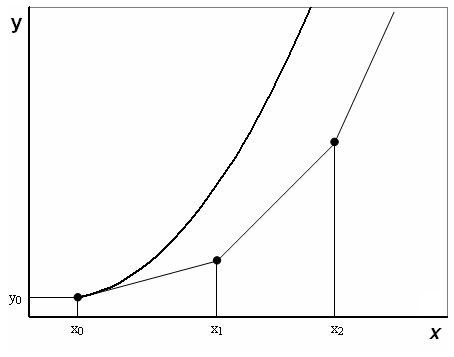
Рис. 7.1. Метод Эйлера

На каждом шаге метода Эйлера решение 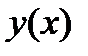определяется с погрешностью за счет отбрасывания членов ряда Тейлора, пропорциональных 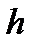в степени выше первой. Это означает, что метод Эйлера имеет второй порядок локальной погрешности. Глобальная погрешность имеет первый порядок. При постоянном шаге 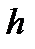для оценки глобальной погрешности применима первая формула Рунге (6.15)

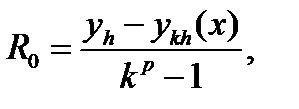(7.8)

где 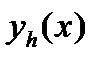– приближенное решение дифференциального уравнения в точке 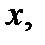полученное с шагом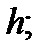 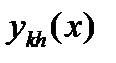– приближенное решение того же уравнения с шагом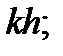 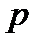– порядок метода.

Формула (7.8) позволяет опытным путем определить шаг 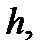обеспечивающий требуемую точность решения 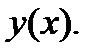Так же, как и при вычислении определенных интегралов, можно осуществлять автоматическое изменение шага в процессе интегрирования дифференциального уравнения.

Для уточнения решения применима вторая формула Рунге (6.16)

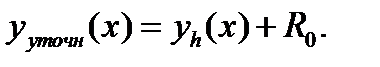(7.9)

Формула Эйлера (7.7) обобщается для системы обыкновенных дифференциальных уравнений, записанных в форме Коши (7.3) с начальными условиями

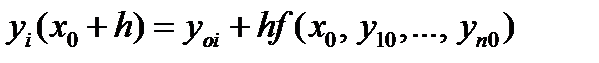. (7.10)

Метод Эйлера дает сравнительно низкую точность,так как имеет первый порядок.