Потоки с ограниченным последствием (потоки Пальма)

Другим обобщением простейшего потока является поток Пальма.

Определение: Потоком Пальма называется поток, обладающий свойствами стационарности, ординарности и независимости интервалов времени Т между событиями.

Требование независимости интервалов Т является более слабым чем требование без последствия, поэтому такие потоки называют также потоками с ограниченными последствиями.

Теорема: пусть в систему поступает поток заявок типа Пальма. Заявка, заставшая все каналы занятыми, получает отказ. Если при этом время обслуживания имеет показательный закон распределения, то поток не обслуженных заявок является потоком Пальма.

Простейший поток является частным случаем потока Пальма. Его независимые интервалы распределены по показательному закону.

Еще одним примером потоков Пальма являются потоки Эрланга, которые могут быть получены следующим образом:

Если из простейшего потока исключается каждое второе требование, то оставшийся поток образует поток второго порядка, если в потоке сохраняется каждое третье, то это – поток третьего порядка и т.д. Для потока к-го порядка функция плотности для интервала Т имеет вид:

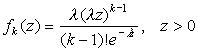(6)

C увеличением порядка k функция f_k(х) убывает, но М[Т] возрастает:

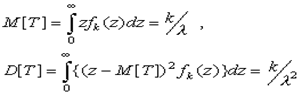
При достаточо большом k (практически при k-5) поток Эрланга k-ого порядка можно считать нормальным с указанными М[T] и D[T]. Это следует из того, что интервал времени Т между двумя последовательными событиями в потоке Эрланга k-ого порядка представляет собой сумму k независимых случайных величин с одним законом распределения. Тогда на основании центральной предельной теоремы теории вероятностей имеем доказательство утверждения.

Задавая различные значения k в (6) можно получить потоки, обладающие различным последействием – от полного его отсутствия (k=1) до полной функциональной связи между моментами появления событий (регулярный поток).

На самом деле: при k=1 получаем простейший поток, а при l =const и при k 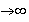поток Эрланга приближается к регулярному.

Свойства потоков Эрланга дает возможность широкого применения этой математической модели.

Потоки восстановления

На практике нередко приходится сталкиваться с потоками, получившими название потоков восстановления. Примером образования такого потока является ситуация, когда в состоянии непрерывной работы должно находиться устройство. Как только оно перестает выполнять свои функции (старение, поломка) его заменяют на такое же, но новое. Моменты замены t_k, k=1,2, … являются случайными, так как длительность безотказной работы каждого устройства тоже величина случайная, независимая и имеет свое распределение F(z). В литературе такие потоки обозначают GI – общий входящий поток (general input).

Для потоков восстановления существует большое число разнообразных задач; в частности задача определения вероятности того, что в течении заданного промежутка времени T появится k событий потока. Простых формул, которые были выведены для простейшего потока, здесь уже нет.

Интересными для практики являются потоки, которые с течениями времени “редеют”, проходя через последовательность приборов обслуживания. Примером этого может быть деталь, которая проходит ряд операций и на каждой операции есть вероятность обнаружения скрытого дефекта. В таких случаях деталь устраняется, а первоначальный поток редеет. Еще одним примером может служить исправление последовательно во времени текста несколькими корректорами. При этом количество незамеченных опечаток редеет. Венгерским математиком А.Реньи был получен интересный результат, который заключается в следующем. Поток восстановления подвергается операции: каждое требование остается в потоке с вероятностью q и выбрасывается из потока с вероятностью p=1-q. Одновременно производится изменение масштаба времени: за единицу масштаба считается промежуток длиной q^-1. Если это двойное преобразование обозначить символом R_q, то последовательное проведение преобразований R_q1 , R_{q2 ,} …, R_qn эквивалентно одному преобразованию R_q1q2…qn . Теорема Реньи состоит в том, что если длительность безотказной работы распределена по закону F(х) имеет конечное математическое ожидание М и

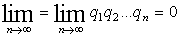
то последовательность редеющих потоков стремится к простейшему пуассоновскому потоку.

Таким образом, в определенных условиях потоки восстановления становятся простейшими, что еще раз подтверждает справедливость теоремы Хинчина.

Термины и определения