Поясните понятие «транспортная задача», постройте модель транспортной задачи, охарактеризуйте её типы
Транспортная задача (задача Монжа — Канторовича) — задача об оптимальном плане перевозок продукта(-ов) из пунктов отправления в пункты потребления. Разработка и применение оптимальных схем грузовых потоков позволяют снизить затраты на перевозки. Транспортная задача является по теории сложности вычислений NP-сложной или входит в класс сложности NP. Когда суммарный объём предложений (грузов, имеющихся в пунктах отправления) не равен общему объёму спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной.
29.Охарактеризуйте методы решения транспортной задачи. Приведите пример решения транспортной задачи.
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из т пунктов отправления 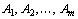 в п пунктов назначения
в п пунктов назначения 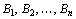 . При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через
. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через 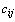 тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через
тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через 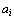 – запасы груза в i-м пункте отправления, через
– запасы груза в i-м пункте отправления, через 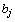 – потребности в грузе в j–м пункте назначения, а через
– потребности в грузе в j–м пункте назначения, а через 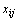 – количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции
– количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции
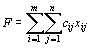 (63)при условиях
(63)при условиях 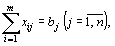 (64)
(64) 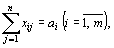 (65)
(65)
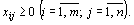 (66)Поскольку переменные
(66)Поскольку переменные 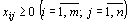 удовлетворяют системам линейных уравнений (64) и (65) и условию неотрицательности (66), обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки. Определение 15. Всякое неотрицательное решение систем линейных уравнений (64) и (65), определяемое матрицей
удовлетворяют системам линейных уравнений (64) и (65) и условию неотрицательности (66), обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки. Определение 15. Всякое неотрицательное решение систем линейных уравнений (64) и (65), определяемое матрицей 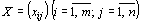 , называется планом транспортной задачи.Определение 16.
, называется планом транспортной задачи.Определение 16.
План 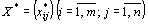 , при котором функция (63) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
, при котором функция (63) принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
Обычно исходные данные транспортной задачи записывают в виде таблицы.
Очевидно, общее наличие груза у поставщиков равно 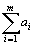 , а общая потребность в грузе в пунктах назначения равна
, а общая потребность в грузе в пунктах назначения равна 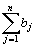 единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т. е.
единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т. е. 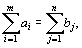 (67)то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.
(67)то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.
Теорема Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т. е. чтобы выполнялось равенство.В случае превышения запаса над потребностью, т. е. 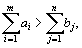 вводится фиктивный (n+1)–й пункт назначения с потребностью
вводится фиктивный (n+1)–й пункт назначения с потребностью 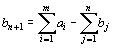 и соответствующие тарифы считаются равными нулю:
и соответствующие тарифы считаются равными нулю: 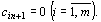 Полученная задача является транспортной задачей, для которой выполняется равенство (67).
Полученная задача является транспортной задачей, для которой выполняется равенство (67).
Число переменных 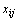 в транспортной задаче с т пунктами отправления и п пунктами назначения равно пт, а число уравнений в системах (64) и (65) равно п+т. Так как мы предполагаем, что выполняется условие (67), то число линейно независимых уравнений равно п+т–1. Следовательно, опорный план транспортной задачи может иметь не более п+т–1 отличных от нуля неизвестных.
в транспортной задаче с т пунктами отправления и п пунктами назначения равно пт, а число уравнений в системах (64) и (65) равно п+т. Так как мы предполагаем, что выполняется условие (67), то число линейно независимых уравнений равно п+т–1. Следовательно, опорный план транспортной задачи может иметь не более п+т–1 отличных от нуля неизвестных.
Если в опорном плане число отличных от нуля компонент равно в точности п+т–1, то план является невырожденным, а если меньше – то вырожденным.
Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом.
Для определения оптимального плана транспортной задачи можно использовать изложенные выше методы.
