Индивидуальные задания. Решите систему линейных уравнений:

Решите систему линейных уравнений:

а) методом Крамера;

b) с помощью обратной матрицы.

Сделайте проверку.

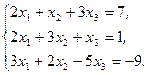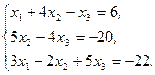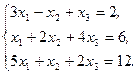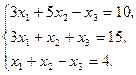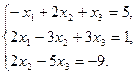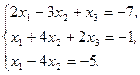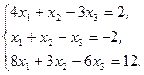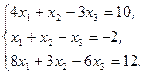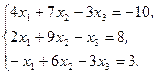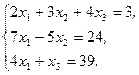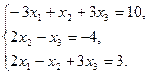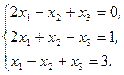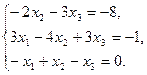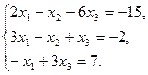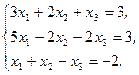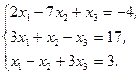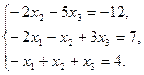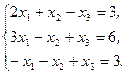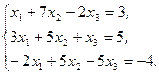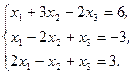Лабораторная работа № 13
Решение задач оптимизации

Задачи оптимизации занимают очень важное место в бизнесе, производстве, прогнозировании. Условно эти задачи можно разделить на следующие категории:

· транспортная задача – минимизация расходов на транспортировку товаров;

· задача о назначениях – составление штатного расписания с минимизацией денежных затрат на заработную плату или времени выполнения работ;

· задачи оптимизации производства – максимизация выпуска товаров при ограничениях на сырье для производства этих товаров.

Прежде, чем искать оптимальное решение задачи необходимо построить ее математическую модель, т.е. осуществить перевод условия и решения на четкий язык математических отношений.

Задача оптимизации в общем виде формулируется следующим образом.

Найти значения переменных x₁, x₂, … , x_n, такие, что целевая функция f(x₁, x₂, … , x_n) примет максимальное, минимальное или заданное значения при ограничениях вида g(x₁, x₂, … , x_n).

Таким образом, задача оптимизации содержит три основных компонента:

· переменные x₁, x₂, … , x_n – определяемые величины;

· целевая функция – это цель, записанная математически в виде функции от переменных, принимающая максимальное, минимальное или заданное значения;

· ограничения – условия или соотношения, которым должны удовлетворять переменные.

MS Excel предоставляет возможность решения оптимизационных задач с помощью надстройки Поиск решения. При этом после создания математической модели на рабочем листе Excel создается табличная модель, где в отдельных ячейках содержаться переменные решения, в отдельные ячейки записаны формулы, по которым будут вычисляться целевая функция и функции ограничений.

Продемонстрируем эту возможность на примере решения следующей транспортной задачи.

Пример 1.Компания «Атлант» хранит свою продукцию на трех складах (первом, втором и третьем), расположенных в разных частях города. На этих складах хранится продукция в количествах 1000, 3000 и 2500 штук соответственно. Продукцию необходимо доставить четырем оптовым покупателям «Урал», «Купец», «Гелиос» и «Меркурий» с минимальными затратами, заявки которых составляют 1300, 800, 2700 и 1700 штук соответственно. Склады оптовых покупателей также расположены в разных частях города. Стоимости (в рублях) доставки одной штуки продукции со складов компании на склады покупателей показаны в следующей таблице.

Склады компании	Оптовые покупатели
«Урал»	«Купец»	«Гелиос»	«Меркурий»
№1
№2
№3

1. Построим математическую модель задачи: определим переменные, целевую функцию и ограничения.

Пусть:

· x₁₁, x₁₂, x₁₃, x₁₄, x₂₁, x₂₂, x₂₃, x₂₄, x₃₁, x₃₂, x₃₃, x₃₄ – количество продукции, перевозимой со складов компании на соответствующие склады покупателей;

· z=50 x₁₁ + 150 x₁₂ + 60 x₁₃ + 75 x₁₄ + 100 x₂₁ + 30 x₂₂ +100 x₂₃ +40 x₂₄+ +70x₃₁+180 x₃₂ + 210 x₃₃ + 120 x₃₄– целевая функция, общая стоимость доставки грузов покупателям;

· x₁₁ + x₁₂ + x₁₃ + x₁₄=1000,
x₂₁ + x₂₂ +x₂₃ +x₂₄=3000,
x₃₁+x₃₂ + x₃₃ + x₃₄=2500 – ограничения для складов компании;

· x₁₁+ x₂₁ + x₃₁=1300,
x₁₂ + x₂₂ + x₃₂=800,
x₁₃ + x₂₃ + x₃₃=2700,
x₁₄+ x₂₄+ x₃₄=1700– ограничения для складов покупателей.

2. Имеем сбалансированную транспортную задачу, так как спрос покупателей (1300+800+2700+1700=6500) равен предложению производителей (1000+3000+2500=6500).

3. Запустите табличный процессор MS Excel. Переименуйте Лист 1 в Сбалансированная модель.

4. Составьте табличную модель Excel (рис. 49).

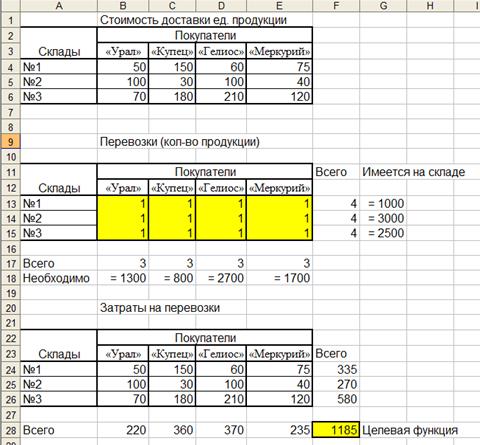
Рис. 49. Сбалансированная модель

5. Последняя таблица не обязательна. Целевую функцию можно было вычислить по формуле:

6. =СУММПРОИЗВ(В4:Е6;В13:Е15).

7. Выделите целевую ячейку и запустите надстройку Поиск решения (Данные 4 Анализ 4 Поиск решения).

8. В появившемся диалоговом окне Поиск решения укажите адреса целевой ячейки, диапазон изменяемых ячеек и ограничения (рис. 50). Целевую ячейку установите равной минимальному значению.

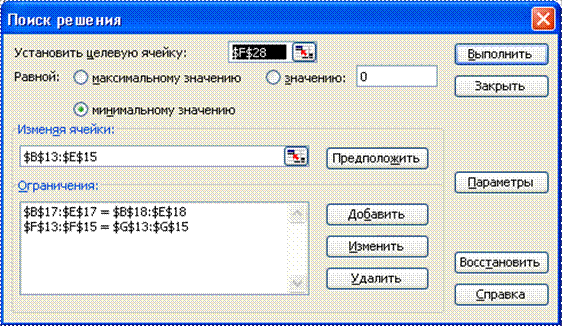
Рис. 50. Диалоговое окно «Поиск решения»

9. В диалоговом окне параметры Поиска решенияустановите флажки Линейная модель, Неотрицательные значения и Автоматическое масштабирование.

10. В диалоговом окне Поиск решения нажмите кнопку Выполнить.

11. Получаем оптимальное решение задачи (рис. 51).

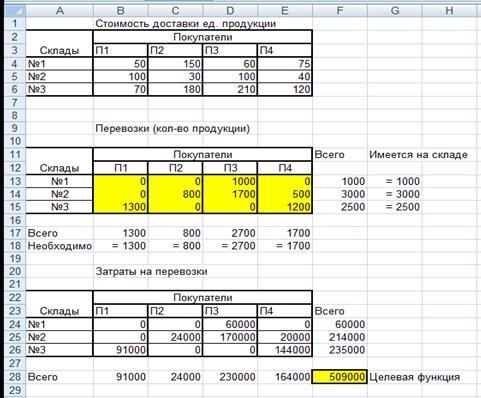
Рис. 51. Оптимальное решение задачи

12. Скопируйте полученную табличную модель на Лист 2 рабочей книги и переименуйте его в Несбалансированная задача.

13. Решим эту же задачу, немного изменив условие.

14. Пусть на складе №1 хранится не 1000 штук продукции, а 500. В таком случае на трех складах компании хранится 6000 штук продукции, покупатели по-прежнему заказывают 6500 штук. Перед нами транспортная задача с дефицитом.

15. Несбалансированная задача решается аналогично сбалансированной. Изменения коснуться только ограничений. Причем в ограничениях для складов покупателей знак «=» заменяется знаком « ≤ ».

16. После выполнения надстройки Поиск решения (рис. 52) получаем, что покупатель «Гелиос» недополучит 500 ед. продукции, а минимальные транспортные расходы составят 479 000 (рис. 53).

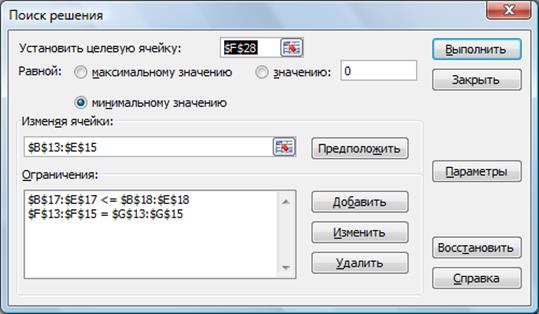
Рис. 52. Поиск решения

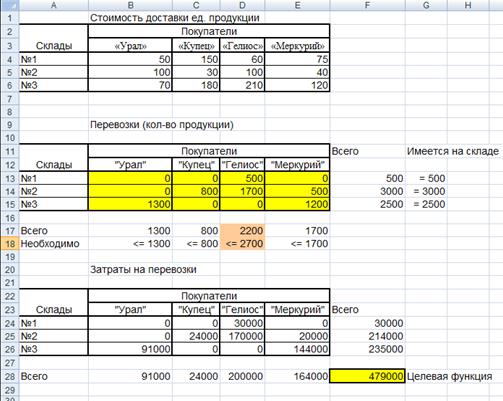
Рис. 53. Оптимальное решение задачи

17. Покажите работу преподавателю.

Частным случаем транспортной задачи является задача о назначениях. В общем виде она формулируется следующим образом: имеется n различных работ и n рабочих. Известны стоимости выполнения каждого вида работ каждым работником. Необходимо так составить штатное расписание, чтобы все работы были выполнены, на выполнение каждой работы назначался только один работник, а затраты на заработную плату были минимальными. В данном случае задача является сбалансированной, так как количество работников равно количеству работ. Ограничения записываются в виде следующих равенств.

· x₁₁ + x₁₂ + …+ x_1n=1,
x₂₁ + x₂₂ +… +x_2n=1,

…
x_n1+x_n2 + … + x_nn=1 – ограничения для работников (каждый работник может выполнять только один вид работ).

· x₁₁ + x₂₁ + …+ x_n1=1,
x₁₂ + x₂₂ +… +x_n2=1,

…
x_1n+x_2n + … + x_nn=1 – ограничения для работ (каждый вид работ может быть выполнен только одним работником).

x_ij – это двоичные переменные, которые могут принимать только два значения: 1, если работник i назначается на выполнение работы j и 0, если не назначается.

Решение задачи о назначениях рассмотрим на примере.

Пример 2.В лингвистическом центре работают 4 преподавателя по следующим направлениям: «Английский для начинающих», «Деловой английский», «Подготовка к ЕГЭ» и «Английский для путешествий». Стоимость академического часа работы каждого преподавателя по каждому курсу представлена в таблице. Составьте оптимальное распределение нагрузки среди сотрудников таким образом, чтобы все курсы были проведены, каждый преподаватель был занят только на одном виде работ, а затраты на заработную плату были минимальными.

№ п/п	ФИО преподавателя	Название курса
Английский для начинающих	Деловой английский	Подготовка к ЕГЭ	Английский для путешествий
	Королев Д. А.
	Воробьева А. С.
	Соловьев Н. А.
	Павлова Р. Г.

1. Построим математическую модель задачи: определим переменные, целевую функцию и ограничения.

Пусть:

· x₁₁, x₁₂, x₁₃, x₁₄, x₂₁, x₂₂, x₂₃, x₂₄, x₃₁, x₃₂, x₃₃, x₃₄ – двоичные переменные, которые могут принимать два значения: 1, если преподаватель i назначается на чтение курса j и 0, если не назначается;

· z=100 x₁₁ + 300 x₁₂ + 110 x₁₃ + 250 x₁₄ + 120 x₂₁ + 180 x₂₂ +100 x₂₃ +150 x₂₄+ +200 x₃₁+200 x₃₂ + 80 x₃₃ + 170 x₃₄ +300 x₄₁+250 x₄₂ + 150 x₄₃ + 230 x₄₄– целевая функция, общая стоимость работ;

· x₁₁ + x₁₂ + x₁₃ + х₁₄=1,
x₂₁ + x₂₂ +x₂₃+ х₂₄=1,
x₃₁ + x₃₂ +x₃₃+ х₃₄=1,
x₄₁ + x₄₂ +x₄₃+ х₄₄=1,
x₁₁ + x₂₁ + x₃₁ + х₄₁=1,
x₂₁ + x₂₂ +x₂₃+ х₂₄=1,
x₁₃ + x₂₃ +x₃₃+ х₄₃=1,
x₁₄ + x₂₄ +x₃₄+ х₄₄=1– ограничения (каждый преподаватель может быть задействован на чтении только одного курса и каждый курс должен быть проведен).

2. На основе математической модели на рабочем листе Excel создадим табличную модель (рис. 54).

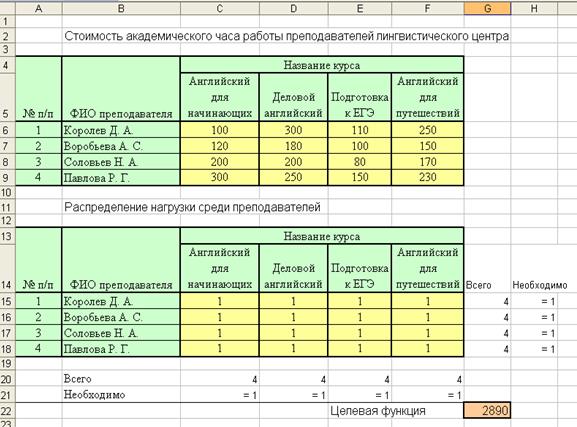
Рис. 54. Задача о назначениях

3. Целевая функция в данном случае вычисляется по формуле =СУММПРОИЗВ(C6:F9;C15:F18).

4. Выделите целевую ячейку и запустите надстройку Поиск решения (Данные 4 Анализ 4 Поиск решения).

5. В появившемся диалоговом окне Поиск решения укажите адреса целевой ячейки, диапазон изменяемых ячеек и ограничения (рис. 55). Целевую ячейку установите равной минимальному значению. В диалоговом окне Параметры поиска решения установите флажки Линейная модель и Автоматическое масштабирование.

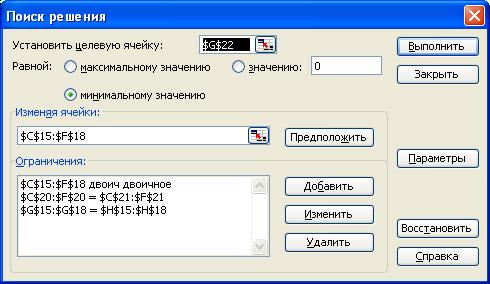
Рис. 55. Поиск решения

6. В диалоговом окне Поиск решения (рис. 55) нажмите кнопку Выполнить.

7. Получаем оптимальное решение задачи (рис. 56).

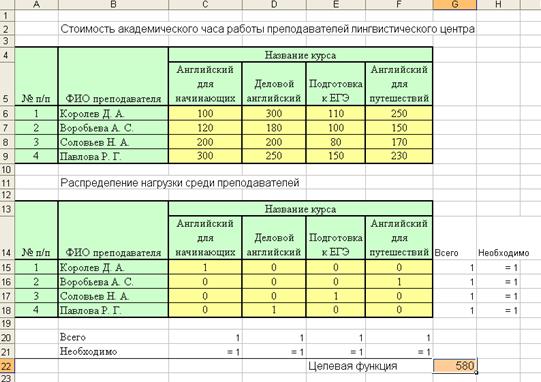
Рис. 56. Оптимальное решение задачи