Числовые характеристики дискретной случайной величины
АУДИТОРНАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ №4
По дисциплине
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
Цель работы:
Научиться получать закон распределения дискретной случайной величины и вычислять ее числовые характеристики с использованием пакета прикладных математических программ Mathcad.
Дискретная случайная величина
Дискретной случайной величиной называется переменная, которая принимает не более чем счетное (конечное или счетное) число значений с заданными вероятностями. При этом сумма вероятностей по всем возможным значениям случайной величины равна единице.
Закон распределения дискретной случайной величины
Закон распределения дискретной случайной величины чаще всего задают в виде таблицы, в которой указываются ее возможные значения и вероятности, с которыми принимаются эти значения. Такая таблица называется рядом распределения (табл. 1).
Таблица 1
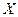 | 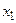 | 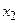 | … | 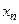 | … |
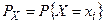 | 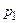 | 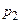 | … | 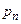 | … |
Для вероятностей 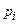 должно выполняться условие
должно выполняться условие
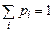 , (1)
, (1)
в котором суммирование ведется по всем возможным значениям случайной величины. В случае бесконечного счетного числа значений случайной величины (1) означает, что числовой ряд 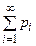 сходится и его сумма равна единице.
сходится и его сумма равна единице.
Если известен ряд распределения дискретной случайной величины 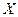 (табл. 1), то ее функция распределения определяется из соотношений:
(табл. 1), то ее функция распределения определяется из соотношений:
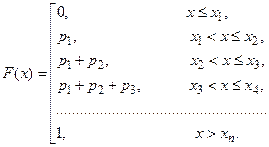 (2)
(2)
С помощью функции распределения находится вероятность
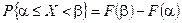 . (3)
. (3)
Числовые характеристики дискретной случайной величины
Математическим ожиданием дискретной случайной величины 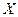 называется число
называется число 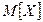 , которое определяется формулой
, которое определяется формулой
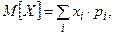 (4)
(4)
в которой 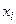 — значения случайной величины;
— значения случайной величины; 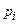 — вероятности, с которыми принимаются эти значения, если числовой ряд
— вероятности, с которыми принимаются эти значения, если числовой ряд 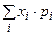 сходится. Иначе математическое ожидание не определено.
сходится. Иначе математическое ожидание не определено.
Модой дискретной случайной величины называется ее возможное значение 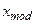 , которое принимается случайной величиной с наибольшей вероятностью.
, которое принимается случайной величиной с наибольшей вероятностью.
Медианой случайной величины 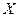 называется возможное значение случайной величины
называется возможное значение случайной величины 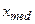 , для которого справедливо соотношение
, для которого справедливо соотношение
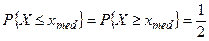 .
.
Дисперсия. Если дискретная случайная величина задана рядом распределения (табл. 1), то ее дисперсия вычисляется по формуле
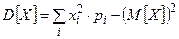 , (5)
, (5)
если определено математическое ожидание 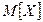 , и случайная величина принимает конечное или счетное число значений, а числовой ряд
, и случайная величина принимает конечное или счетное число значений, а числовой ряд 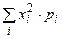 сходится. Иначе дисперсия не определена.
сходится. Иначе дисперсия не определена.
Среднеквадратическим отклонением случайной величины (СКВО) называется неотрицательное число 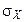 , которое определяется по формуле
, которое определяется по формуле
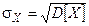 . (6)
. (6)
Задача 1
Случайная величина 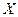 задана рядом распределения в табл. 2.
задана рядом распределения в табл. 2.
Таблица 2
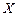 | ||||||
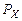 | 0,1 | 0,2 | 0,1 | 0,15 | 0,2 | 0,25 |
Найти закон распределения, вероятность 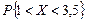 и все числовые характеристики.
и все числовые характеристики.
Решение: Значения случайной величины 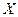 зададим в среде Mathcad в виде вектора
зададим в среде Mathcad в виде вектора 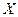 , а соответствующие вероятности — вектором
, а соответствующие вероятности — вектором 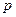 (рис. 1).
(рис. 1).
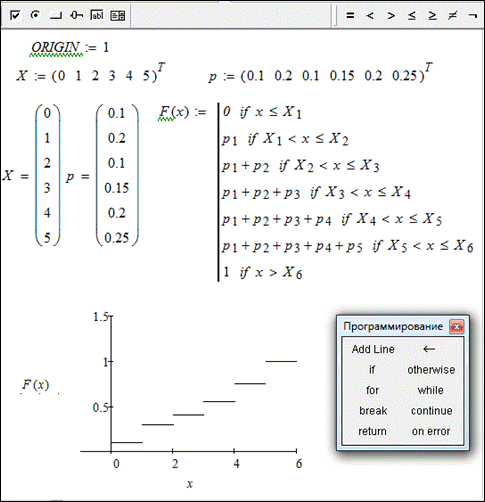
Рис. 1
Векторы 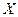 и
и 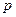 заданы в виде строки–матрицы и транспонированы операцией транспонирования (Т) с панели Матрицы.
заданы в виде строки–матрицы и транспонированы операцией транспонирования (Т) с панели Матрицы.
На рис. 1 показано вычисление среде Mathcad функции 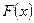 — функции распределения случайной величины
— функции распределения случайной величины 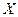 и ее график. Функция
и ее график. Функция 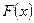 формируется с помощью операторов панели Программирование — Add Line и if. При использовании оператора Add Line следует иметь в виду, что эту «иконку» следует щелкнуть мышью столько раз, сколько должно появиться строк, поскольку внутри оператора присваивания добавлять новые строки уже нельзя. При использовании оператора if все операции отношений нужно набирать на логической панели — на рис. 1 она вверху под главной панелью. При построении графика функции распределения
формируется с помощью операторов панели Программирование — Add Line и if. При использовании оператора Add Line следует иметь в виду, что эту «иконку» следует щелкнуть мышью столько раз, сколько должно появиться строк, поскольку внутри оператора присваивания добавлять новые строки уже нельзя. При использовании оператора if все операции отношений нужно набирать на логической панели — на рис. 1 она вверху под главной панелью. При построении графика функции распределения 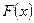 следует в меню Формат в раскрывающемся списке Тип линии выбрать опцию точек (point).
следует в меню Формат в раскрывающемся списке Тип линии выбрать опцию точек (point).
Модальное значение 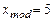 , поскольку вероятность
, поскольку вероятность 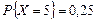 — наибольшая. Учитывая, что
— наибольшая. Учитывая, что 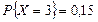 можно представить как
можно представить как 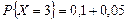 , установим, что
, установим, что
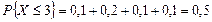 и
и 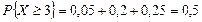 .
.
Тогда по определению 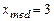 . Остальные числовые характеристики вычислены в среде Mathcad.
. Остальные числовые характеристики вычислены в среде Mathcad.
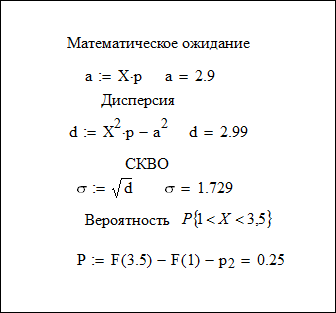
Рис. 2
На рис. 2 по формулам (4) — (6) вычислены: 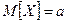 ,
, 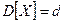 и СКВО
и СКВО 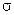 . По формуле (3) найдена вероятность
. По формуле (3) найдена вероятность 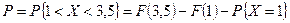 .
.
