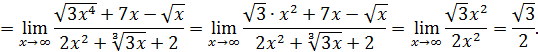Раскрытие неопределённостей от алгебраических функций
Раздел 6. Введение в математический анализ.
1. Предел функции.
2. Раскрытие неопределённостей от алгебраических функций
3. Раскрытие неопределённостей от тригонометрических функций
4. Раскрытие неопределённостей от показательных и логарифмических функций
В данном разделе рассмотрена основная теория математики – теория пределов. Эта теория является фундаментом, на котором построено великолепное сооружение, носящее название «математический анализ».
Математический анализ в настоящее время является незаменимым инструментом исследования в самых различных областях науки и техники. Знания дифференциального и интегрального исчисления сейчас необходимо каждому инженеру и научному работнику. Но для того чтобы изучить математический анализ и научиться правильно его применять, необходимо сначала освоить теорию пределов.
Начало изучения теории пределов положено в элементарной математике, где с помощью предельных переходов определяется длина окружности, объем цилиндра, конуса и т.д. операция предельного перехода является одной из основных операций математического анализа.
Понятие предела часто используется в повседневной жизни. Оно ассоциируется в нашем сознании с числом, к которому приближается значение переменной величины, оставаясь или меньше этого числа, или больше, или изменяясь, принимая то большие , то меньшие значения.
Предел функции
Одним из важнейших понятий математического анализа является понятие предела функции: 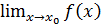 – «предел функции
– «предел функции 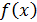 при
при 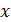 , стремящемся к числу
, стремящемся к числу 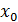 ».,с которым знакомятся уже в школе. Строгое понятие предела мы рассматривать не будем – ведь нашей задачей является научиться вычислять пределы.
».,с которым знакомятся уже в школе. Строгое понятие предела мы рассматривать не будем – ведь нашей задачей является научиться вычислять пределы.
Первое правило, которое мы всегда будем применять при вычислении пределов состоит в том, что начинать вычисление пределов 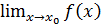 надо с подстановки предельного значения аргумента
надо с подстановки предельного значения аргумента 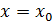 в функцию, стоящую под знаком предела, т.е. с вычисления
в функцию, стоящую под знаком предела, т.е. с вычисления 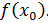 Если
Если 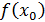 существует, то это число и есть искомый предел.
существует, то это число и есть искомый предел.
Пример 1. Вычислить 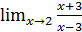 .
.
Решение. 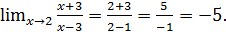
Пример 2. Вычислить 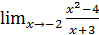 .
.
Решение. 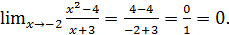
Определение. Если 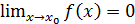 , то функция
, то функция 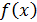 называется бесконечно малой (б.м.) при
называется бесконечно малой (б.м.) при 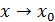 .
.
Так, в примере 2 функция 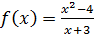 является бесконечно малой (б.м.) при
является бесконечно малой (б.м.) при 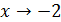 . Заметим, что понятие передела, следовательно, и понятие б.м. функции является локальным понятием, т.е. применённым к определенной точке. В примере 2 функция
. Заметим, что понятие передела, следовательно, и понятие б.м. функции является локальным понятием, т.е. применённым к определенной точке. В примере 2 функция 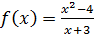 уже не является б.м., например, при
уже не является б.м., например, при 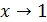 , т.к.
, т.к. 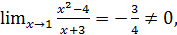 но она вновь становится б.м. при
но она вновь становится б.м. при 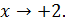
Определение. Если функция 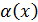 – б.м. при
– б.м. при 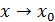 , то функция
, то функция 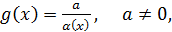 называется бесконечно большой (б.б.) при
называется бесконечно большой (б.б.) при 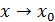 и это обозначается символом бесконечности следующим образом:
и это обозначается символом бесконечности следующим образом:
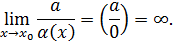
Если функция 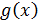 - б.б. при
- б.б. при 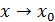 , то функция
, то функция 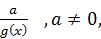 - б.м. при
- б.м. при 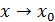 и это записывается следующим образом:
и это записывается следующим образом:
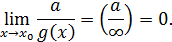
Пример 3. 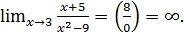
Пример 4. 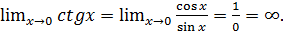
Заметим, что в курсе элементарной математики мы говорили, что «котангенс нуля не существует». Теперь ещё будем говорить, что «котангенс нуля равен бесконечности», что хорошо соответствует графику котангенса – при 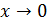 ветви котангенса неограниченно уходят вверх и вниз, т.е. котангенс неограниченно возрастает или убывает («стремится к плюс или минус бесконечности»).
ветви котангенса неограниченно уходят вверх и вниз, т.е. котангенс неограниченно возрастает или убывает («стремится к плюс или минус бесконечности»).
Итак, если при 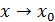 функция неограниченно возрастает (или убывает), кратко записываем, что
функция неограниченно возрастает (или убывает), кратко записываем, что 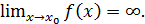 Рассмотрим более интересные примеры.
Рассмотрим более интересные примеры.
Пример 5. Вычислить 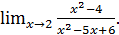
Решение: Начинаем с подстановки предельного значения аргумента:
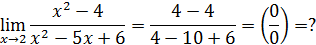
Что же мы должны записать в ответе? Вспоминаем школьное правило: «ноль, делённый на любое число даёт ноль» и только что приобретённое: «любое число, делённое на ноль даёт бесконечность». Получаем разные результаты. Такая ситуация называется неопределённостью, в данном случае типа 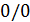 . Мы увидим, что неопределённости могут быть различных типов, и вычисление соответствующих пределов (как говорят, «раскрытие неопределённостей») и составляет нашу основную задачу.
. Мы увидим, что неопределённости могут быть различных типов, и вычисление соответствующих пределов (как говорят, «раскрытие неопределённостей») и составляет нашу основную задачу.
В примере 5 это делается следующим образом:
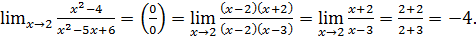
Прежде чем выстраивать теорию, отметим, что все элементарные функции разбиваются на три группы.
Первую группу составляют алгебраические функции, т.е. функции, которые получаются из аргумента 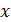 с помощью алгебраических операций, каковыми являются сложение, вычитание, умножение, деление, возведение в степень и извлечение корня. Например,
с помощью алгебраических операций, каковыми являются сложение, вычитание, умножение, деление, возведение в степень и извлечение корня. Например, 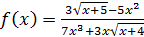 - алгебраическая функция.
- алгебраическая функция.
Вторую группу составляют тригонометрические и обратные тригонометрические функции.
В третью группу входят показательные функции и обратные к ним -логарифмические функции.
Вспомните школьный курс математики – тригонометрические формулы и формулы для показательных и логарифмических функций находятся изолированно друг от друга – у каждой группы функций свои формулы. По этой причине и раскрытие неопределённостей для разных групп функций проводится специфически.
Раскрытие неопределённостей от алгебраических функций.
Начнём с простейшего случая – с отношения двух многочленов:
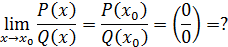
\Здесь воспользуемся теоремой Безу: если 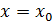 - корень многочлена
- корень многочлена 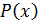 , то
, то 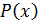 делится без остатка на
делится без остатка на 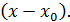 Поэтому:
Поэтому:
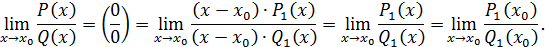
Именно так мы решили пример 5 и уже на этом примере,
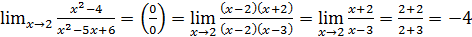 ,
,
увидели, что из двух сомножителей в числителе и знаменателе, лишь сомножитель 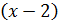 является источником появления неопределённости. После сокращения на этот множитель неопределённость исчезла.
является источником появления неопределённости. После сокращения на этот множитель неопределённость исчезла.
Таким образом, можно обозначить цель наших преобразований: выделить в числителе и знаменателе простейший источник появления определённости: множитель 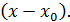
Пример 6. 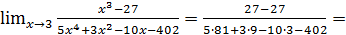
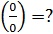
Нам ясна цель – в числителе и знаменателе выделить множитель 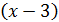 , поскольку и числитель и знаменатель делится без остатка на
, поскольку и числитель и знаменатель делится без остатка на 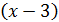 .В числителе удобно применить формулу «разности кубов»:
.В числителе удобно применить формулу «разности кубов»: 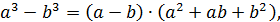 по которой
по которой 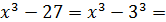
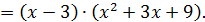 В знаменателе так просто выделить сомножитель
В знаменателе так просто выделить сомножитель 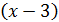 не удаётся, поэтому делим «уголком»:
не удаётся, поэтому делим «уголком»:
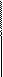



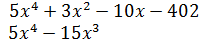
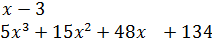


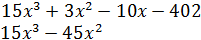


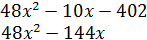


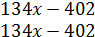
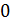
Деление завершено:
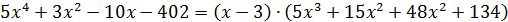
Теперь вычисляем предел:
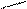
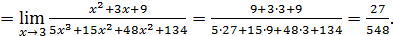
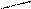
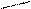 Пример 7.
Пример 7. 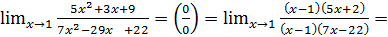
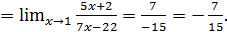
Заметим, что в этом примере для того, чтобы числитель и знаменатель разложить на множители с выделением 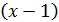 , не обязательно решать квадратные уравнения или делить «уголком», - вторые сомножители легко подобрать. Переходим к более сложным случаям, когда присутствуют радикалы (иррациональности).
, не обязательно решать квадратные уравнения или делить «уголком», - вторые сомножители легко подобрать. Переходим к более сложным случаям, когда присутствуют радикалы (иррациональности).
Пример 8. Вычислить 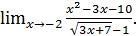
Решение. Нетрудно обнаружить, что имеем неопределённость типа «ноль делить на ноль»  Что делать с числителем нам ясно – надо выделить сомножитель
Что делать с числителем нам ясно – надо выделить сомножитель 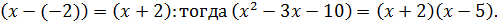
В знаменателе имеем иррациональность, от которой следует «избавиться», воспользовавшись формулой «разности квадратов» 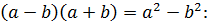 домножим знаменатель
домножим знаменатель 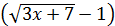 на сопряжённое выражение
на сопряжённое выражение 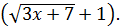 Тогда
Тогда 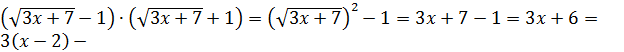 «избавились» от иррациональности.
«избавились» от иррациональности.
Разумеется, чтобы не нарушить равенства в пределе на такое же выражение 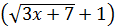 надо домножить и числитель. В совокупности решение выглядит следующим образом:
надо домножить и числитель. В совокупности решение выглядит следующим образом:
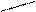
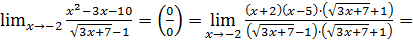
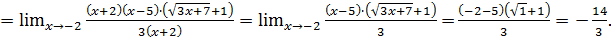
Пример 9. 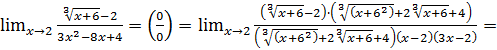
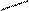
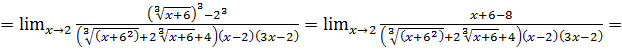
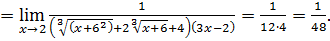
В этом примере мы использовали в числителе формулу «разности кубов».
До сих пор мы рассматривали пределы, когда аргумент 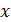 стремится к конечному числу
стремится к конечному числу 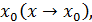 и различными способами выделяли сомножитель
и различными способами выделяли сомножитель 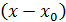 - простейший источник появления неопределённости.
- простейший источник появления неопределённости.
Но сам аргумент 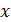 может неограниченно возрастать, т.е. стремиться к бесконечности
может неограниченно возрастать, т.е. стремиться к бесконечности 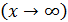 . Рассмотрим такие пределы.
. Рассмотрим такие пределы.
Определение. Пусть имеются две бесконечно малые (б.м.) функции 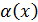 и
и 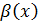 при
при 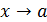 (где
(где 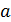 может быть как конечным числом
может быть как конечным числом 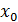 так и
так и 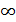 ). Функции
). Функции 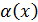 и
и 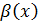 называются эквивалентными б.м. при
называются эквивалентными б.м. при 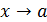 , если предел их отношения равен единице:
, если предел их отношения равен единице:
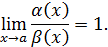
Обозначение: 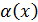
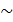
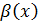 при
при 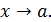
Теорема 1. Под знаком предела одну бесконечно малую функцию можно заменить другой, ей эквивалентной.
Доказательство. Пусть имеется неопределённость типа 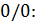
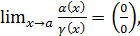 и известно, что
и известно, что 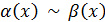 при
при 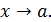 Тогда
Тогда 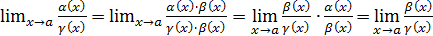 , т.е.
, т.е. 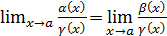 что и требовалось доказать.
что и требовалось доказать.
Мы неоднократно убедимся в полезности этой теоремы. Для бесконечно больших функций аналогично:
определение: Две бесконечно большие (б.б.) функции 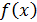 и
и 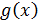 при
при 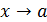 называются эквивалентными, если предел их отношения равен единице:
называются эквивалентными, если предел их отношения равен единице: 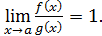
Теорема 2. Под знаком предела одну бесконечно большую фукнкцию можно заменять другой, ей эквивалентной.
Доказательство аналогично.
Теорема 3. Всякий многочлен при 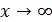 эквивалентен своему старшему члену.
эквивалентен своему старшему члену.
Доказательство.  следовательно,
следовательно, 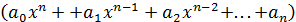
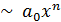 при
при 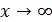 .
.
Теперь переходим к примерам.
Пример 10. Вычислить 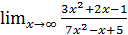 .
.
Решение. По доказанной теореме 3 многочлен при 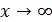 эквивалентен своему старшему члену:
эквивалентен своему старшему члену: 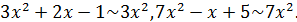 Под знаком предела одну б.б. функцию можно заменять другой, ей эквивалентной. Заменим многочлены их старшими членами и получаем результат. Оформим эти выкладки следующим образом.
Под знаком предела одну б.б. функцию можно заменять другой, ей эквивалентной. Заменим многочлены их старшими членами и получаем результат. Оформим эти выкладки следующим образом.
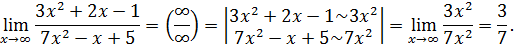
Пример 11. 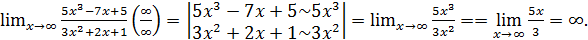
Пример 12. 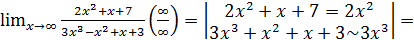
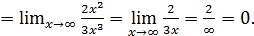
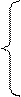 Последние три примера позволяют сформулировать общее правило для предела отношения двух многочленов при
Последние три примера позволяют сформулировать общее правило для предела отношения двух многочленов при 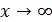 :
:
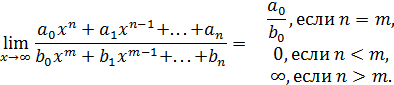
Пример 13. Вычислить 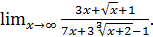
Решение. В этом примере под знаком предела находятся радикалы (иррациональности).
Во-первых, 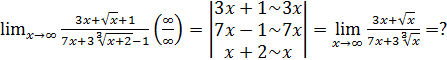
Во – вторых, теорему 3 очевидно можно обобщить для всякой алгебраической функции: при 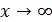 она эквивалентна своему старшему члену, т.е. члену с наивысшей степенью аргумента. Поэтому
она эквивалентна своему старшему члену, т.е. члену с наивысшей степенью аргумента. Поэтому
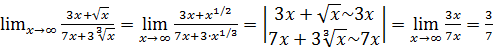 .
.
Пример 14.