А) Определение и способы задания.
Обсуждена на заседании кафедры
Протокол № 17 от
«31» июля 2014 года
I. Цели и задачи занятия
1. Дать определение и способы задания функции, рассмотреть основные характеристики функций, основные элементарные, обратную и сложную функции, параметрическое задание функции и полярные координаты.
2. Показать важность данной темы и воспитывать интерес к изучаемой дисциплине.
3. Развивать у обучающихся познавательный интерес к изучаемой дисциплине.
II. Расчет учебного времени
| Содержание и порядок проведения занятия | Время, мин |
| ВВОДНАЯ ЧАСТЬ ОСНОВНАЯ ЧАСТЬ Учебные вопросы 1. Функция: а) определение и способы задания; б) основные характеристики; в) обратная и сложная функции; г) основные элементарные функции. 2. Параметрический способ задания функции. 3. Полярные координаты. ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ |
III. Литература
основная
1. Шипачев В.С. Высшая математика. Москва «Высшая школа» 2010.
дополнительная
1. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть. – М.: «Рольф», 2005
IV. Учебно-материальное обеспечение
1. Технические средства обучения: видеопроектор, ноутбук, экран.
V. Текст лекции
Вводная часть
Одним из основных математических понятий является понятие функции при изучении различных явлений природы и решение технических задач, а следовательно, и в математике приходится рассматривать изменение одной величины в зависимости от изменения другой. Так, например, при движении путь рассматривается как величина, зависящая от времени. Понятие функции связано с установлением зависимости между элементами двух множеств.
Учебные вопросы
1. Функция:
а) определение и способы задания;
б) основные характеристики;
в) обратная и сложная функции;
г) основные элементарные функции.
2. Параметрический способ задания функции.
3. Полярные координаты.
I. Функция.
а) Определение и способы задания.
Сформулируем определение понятия «функция»:
Определение: Пусть даны два множества 
и 
(непустых). Соответствие 
, которое каждому элементу 
сопоставляет один и только один элемент 
называется функцией и записывается 
или 
(говорят еще, что функция отображает множество на множество ).
а), б) – функции; в) – нет; г) – нет (не единственный ).
Если элементами множеств и являются действительные числа (т.е. 
, 
), то функцию называют числовой.
Множество называется областью определения функции и обозначается 
; множество всех называется множеством значений функции и обозначается 
.
Переменная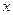 
называется аргументом или независимой переменной, а 
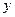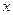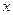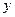– значением функции (функцией) или зависимой переменной (от ). Относительно самих величин и говорят, что они находятся в функциональной зависимости (иногда пишут 
).
Частное значение функции 
при 
записывают так: 
(или 
). Например, если 
, то 
, 
.
Чтобы задать функцию, необходимо указать правило, позволяющее, зная 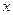, находить соответствующее значение .
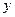Наиболее часто встречаются следующие способы задания функции: аналитический, графический, табличный.
Аналитический способ: функция задается в виде одной или нескольких формул или уравнений.
Например, 
; 
; 
.
Если область определения функции не указывается, то предполагается, что она совпадает с множеством всех значений аргумента, при которых формула имеет смысл, например, для 
, 
.
Аналитический способ является наиболее совершенным, т.к. к нему приложены методы математического анализа, позволяющие полностью исследовать функцию.
Графический способ: задается график функции.
Графиком функции 
называется множество всех точек 
, абсциссами которых являются аргументы ( ), а ординатами – соответствующие им значения функции.
Например, графиком функции 
является прямая.
Графический способ удобен, когда задать функцию аналитически трудно. Часто графики вычерчиваются автоматически самопишущими приборами или изображаются на экране дисплея. Непосредственно из графика можно находить значения функции, соответствующие тем или иным значениям аргумента. По графику можно наглядно судить о поведении и свойствах функции (четность, монотонность, ограниченность, периодичность и т.д.).
Преимуществом графического способа является его наглядность, недостатком – его неточность.
Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известны таблицы значений тригонометрических функций, логарифмические таблицы. На практике часто приходится пользоваться таблицами значений функции, полученных опытным путем или в результате наблюдений.